Sequent-Type Calculi for Systems of Nonmonotonic Paraconsistent Logics

Paraconsistent logics constitute an important class of formalisms dealing with non-trivial reasoning from inconsistent premisses. In this paper, we introduce uniform axiomatisations for a family of nonmonotonic paraconsistent logics based on minimal inconsistency in terms of sequent-type proof systems. The latter are prominent and widely-used forms of calculi well-suited for analysing proof search. In particular, we provide sequent-type calculi for Priest's three-valued minimally inconsistent logic of paradox, and for four-valued paraconsistent inference relations due to Arieli and Avron. Our calculi follow the sequent method first introduced in the context of nonmonotonic reasoning by Bonatti and Olivetti, whose distinguishing feature is the use of a so-called rejection calculus for axiomatising invalid formulas. In fact, we present a general method to obtain sequent systems for any many-valued logic based on minimal inconsistency, yielding the calculi for the logics of Priest and of Arieli and Avron as special instances.

Stepwise Debugging of Answer-Set Programs

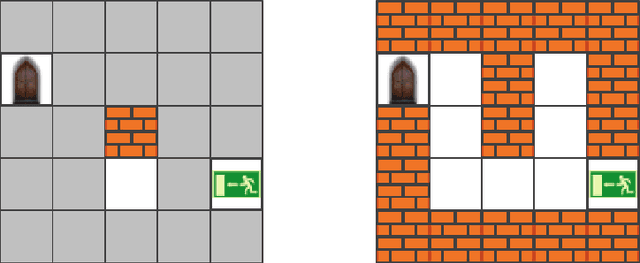
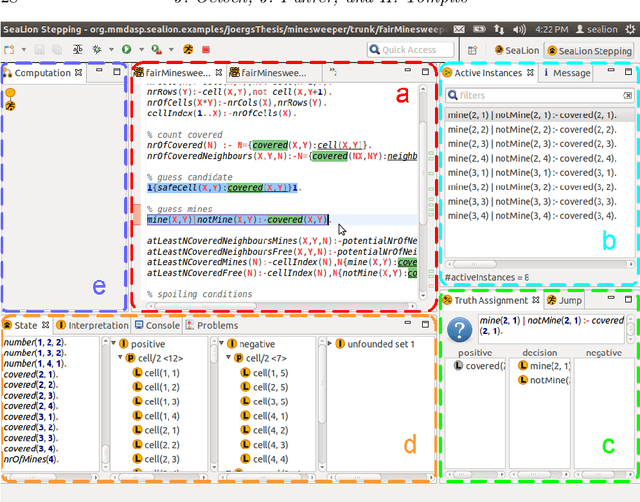
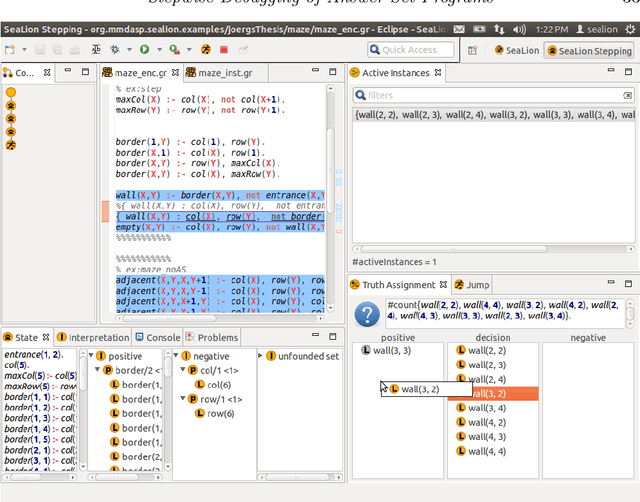
We introduce a stepping methodology for answer-set programming (ASP) that allows for debugging answer-set programs and is based on the stepwise application of rules. Similar to debugging in imperative languages, where the behaviour of a program is observed during a step-by-step execution, stepping for ASP allows for observing the effects that rule applications have in the computation of an answer set. While the approach is inspired from debugging in imperative programming, it is conceptually different to stepping in other paradigms due to non-determinism and declarativity that are inherent to ASP. In particular, unlike statements in an imperative program that are executed following a strict control flow, there is no predetermined order in which to consider rules in ASP during a computation. In our approach, the user is free to decide which rule to consider active in the next step following his or her intuition. This way, one can focus on interesting parts of the debugging search space. Bugs are detected during stepping by revealing differences between the actual semantics of the program and the expectations of the user. As a solid formal basis for stepping, we develop a framework of computations for answer-set programs. For fully supporting different solver languages, we build our framework on an abstract ASP language that is sufficiently general to capture different solver languages. To this end, we make use of abstract constraints as an established abstraction for popular language constructs such as aggregates. Stepping has been implemented in SeaLion, an integrated development environment for ASP. We illustrate stepping using an example scenario and discuss the stepping plugin of SeaLion. Moreover, we elaborate on methodological aspects and the embedding of stepping in the ASP development process.

Modularity Aspects of Disjunctive Stable Models

Practically all programming languages allow the programmer to split a program into several modules which brings along several advantages in software development. In this paper, we are interested in the area of answer-set programming where fully declarative and nonmonotonic languages are applied. In this context, obtaining a modular structure for programs is by no means straightforward since the output of an entire program cannot in general be composed from the output of its components. To better understand the effects of disjunctive information on modularity we restrict the scope of analysis to the case of disjunctive logic programs (DLPs) subject to stable-model semantics. We define the notion of a DLP-function, where a well-defined input/output interface is provided, and establish a novel module theorem which indicates the compositionality of stable-model semantics for DLP-functions. The module theorem extends the well-known splitting-set theorem and enables the decomposition of DLP-functions given their strongly connected components based on positive dependencies induced by rules. In this setting, it is also possible to split shared disjunctive rules among components using a generalized shifting technique. The concept of modular equivalence is introduced for the mutual comparison of DLP-functions using a generalization of a translation-based verification method.

Annotating Answer-Set Programs in LANA?

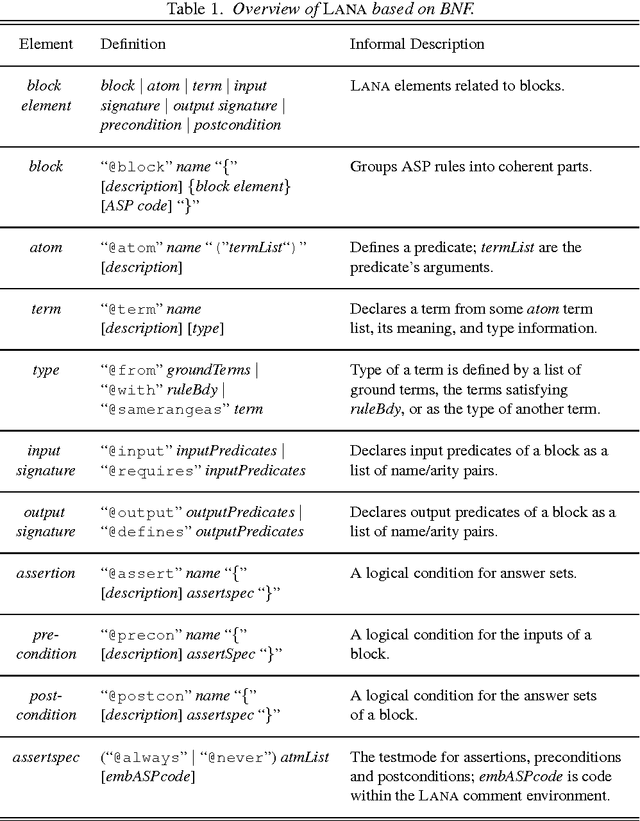
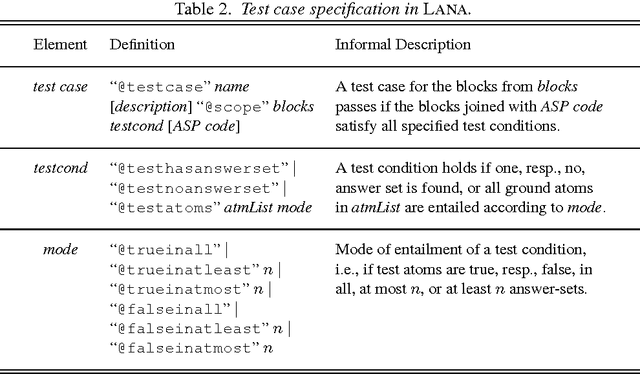
While past research in answer-set programming (ASP) mainly focused on theory, ASP solver technology, and applications, the present work situates itself in the context of a quite recent research trend: development support for ASP. In particular, we propose to augment answer-set programs with additional meta-information formulated in a dedicated annotation language, called LANA. This language allows the grouping of rules into coherent blocks and to specify language signatures, types, pre- and postconditions, as well as unit tests for such blocks. While these annotations are invisible to an ASP solver, as they take the form of program comments, they can be interpreted by tools for documentation, testing, and verification purposes, as well as to eliminate sources of common programming errors by realising syntax checking or code completion features. To demonstrate its versatility, we introduce two such tools, viz. (i) ASPDOC, for generating an HTML documentation for a program based on the annotated information, and (ii) ASPUNIT, for running and monitoring unit tests on program blocks. LANA is also exploited in the SeaLion system, an integrated development environment for ASP based on Eclipse. To appear in Theory and Practice of Logic Programming

Extending Object-Oriented Languages by Declarative Specifications of Complex Objects using Answer-Set Programming

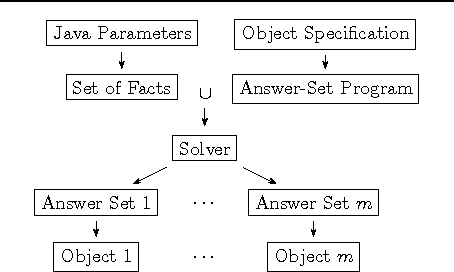
Many applications require complexly structured data objects. Developing new or adapting existing algorithmic solutions for creating such objects can be a non-trivial and costly task if the considered objects are subject to different application-specific constraints. Often, however, it is comparatively easy to declaratively describe the required objects. In this paper, we propose to use answer-set programming (ASP)---a well-established declarative programming paradigm from the area of artificial intelligence---for instantiating objects in standard object-oriented programming languages. In particular, we extend Java with declarative specifications from which the required objects can be automatically generated using available ASP solver technology.

Kara: A System for Visualising and Visual Editing of Interpretations for Answer-Set Programs

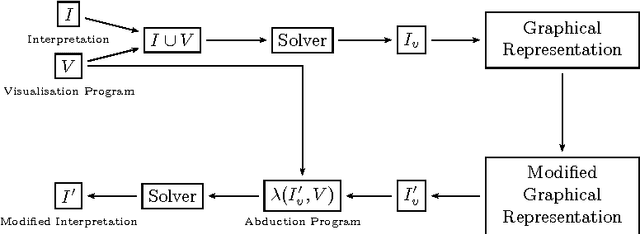
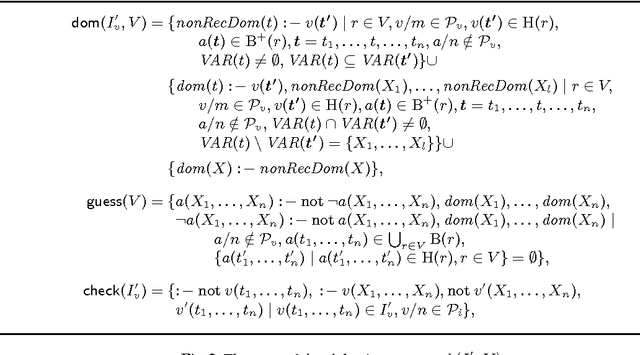
In answer-set programming (ASP), the solutions of a problem are encoded in dedicated models, called answer sets, of a logical theory. These answer sets are computed from the program that represents the theory by means of an ASP solver and returned to the user as sets of ground first-order literals. As this type of representation is often cumbersome for the user to interpret, tools like ASPVIZ and IDPDraw were developed that allow for visualising answer sets. The tool Kara, introduced in this paper, follows these approaches, using ASP itself as a language for defining visualisations of interpretations. Unlike existing tools that position graphic primitives according to static coordinates only, Kara allows for more high-level specifications, supporting graph structures, grids, and relative positioning of graphical elements. Moreover, generalising the functionality of previous tools, Kara provides modifiable visualisations such that interpretations can be manipulated by graphically editing their visualisations. This is realised by resorting to abductive reasoning techniques. Kara is part of SeaLion, a forthcoming integrated development environment (IDE) for ASP.

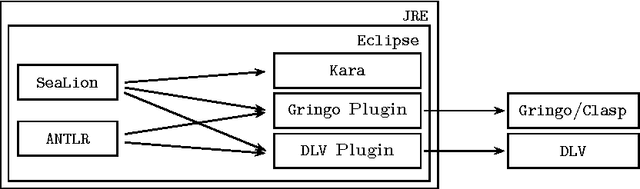
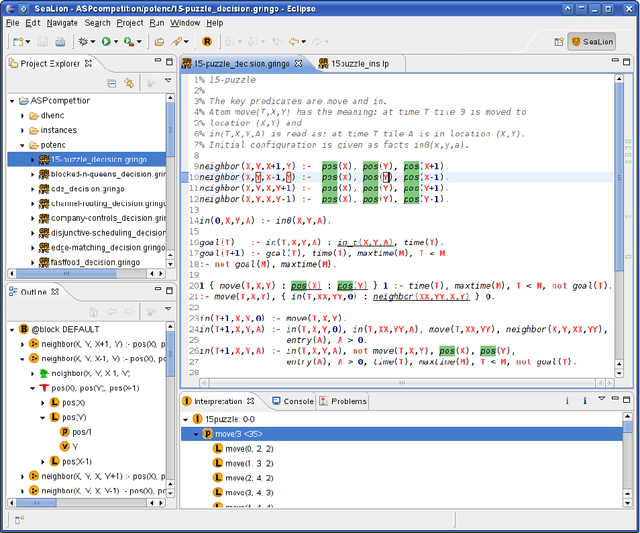
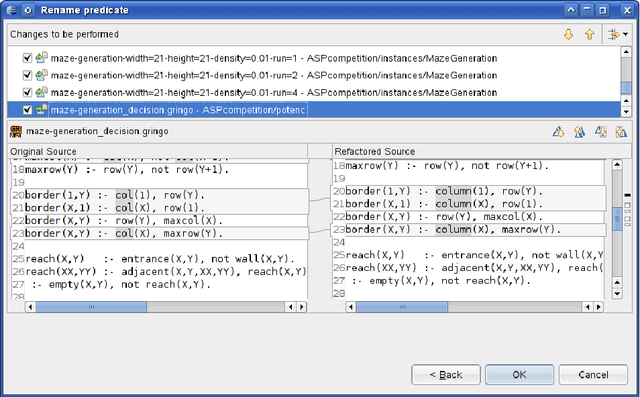
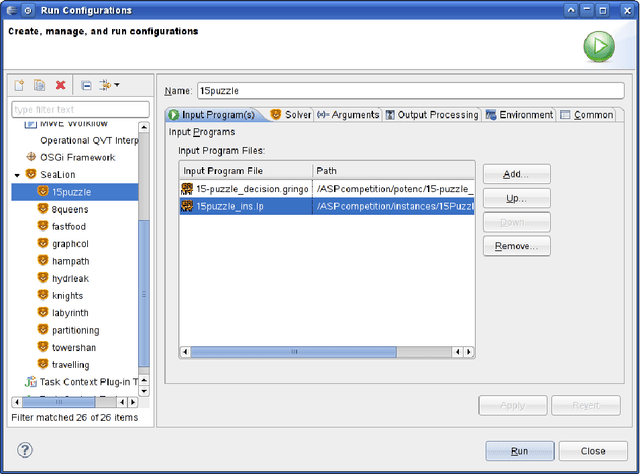
The SeaLion has Landed: An IDE for Answer-Set Programming---Preliminary Report

We report about the current state and designated features of the tool SeaLion, aimed to serve as an integrated development environment (IDE) for answer-set programming (ASP). A main goal of SeaLion is to provide a user-friendly environment for supporting a developer to write, evaluate, debug, and test answer-set programs. To this end, new support techniques have to be developed that suit the requirements of the answer-set semantics and meet the constraints of practical applicability. In this respect, SeaLion benefits from the research results of a project on methods and methodologies for answer-set program development in whose context SeaLion is realised. Currently, the tool provides source-code editors for the languages of Gringo and DLV that offer syntax highlighting, syntax checking, and a visual program outline. Further implemented features are support for external solvers and visualisation as well as visual editing of answer sets. SeaLion comes as a plugin of the popular Eclipse platform and provides itself interfaces for future extensions of the IDE.

Embedding Non-Ground Logic Programs into Autoepistemic Logic for Knowledge Base Combination

In the context of the Semantic Web, several approaches to the combination of ontologies, given in terms of theories of classical first-order logic and rule bases, have been proposed. They either cast rules into classical logic or limit the interaction between rules and ontologies. Autoepistemic logic (AEL) is an attractive formalism which allows to overcome these limitations, by serving as a uniform host language to embed ontologies and nonmonotonic logic programs into it. For the latter, so far only the propositional setting has been considered. In this paper, we present three embeddings of normal and three embeddings of disjunctive non-ground logic programs under the stable model semantics into first-order AEL. While the embeddings all correspond with respect to objective ground atoms, differences arise when considering non-atomic formulas and combinations with first-order theories. We compare the embeddings with respect to stable expansions and autoepistemic consequences, considering the embeddings by themselves, as well as combinations with classical theories. Our results reveal differences and correspondences of the embeddings and provide useful guidance in the choice of a particular embedding for knowledge combination.

A general approach to belief change in answer set programming

We address the problem of belief change in (nonmonotonic) logic programming under answer set semantics. Unlike previous approaches to belief change in logic programming, our formal techniques are analogous to those of distance-based belief revision in propositional logic. In developing our results, we build upon the model theory of logic programs furnished by SE models. Since SE models provide a formal, monotonic characterisation of logic programs, we can adapt techniques from the area of belief revision to belief change in logic programs. We introduce methods for revising and merging logic programs, respectively. For the former, we study both subset-based revision as well as cardinality-based revision, and we show that they satisfy the majority of the AGM postulates for revision. For merging, we consider operators following arbitration merging and IC merging, respectively. We also present encodings for computing the revision as well as the merging of logic programs within the same logic programming framework, giving rise to a direct implementation of our approach in terms of off-the-shelf answer set solvers. These encodings reflect in turn the fact that our change operators do not increase the complexity of the base formalism.

Characterising equilibrium logic and nested logic programs: Reductions and complexity

Equilibrium logic is an approach to nonmonotonic reasoning that extends the stable-model and answer-set semantics for logic programs. In particular, it includes the general case of nested logic programs, where arbitrary Boolean combinations are permitted in heads and bodies of rules, as special kinds of theories. In this paper, we present polynomial reductions of the main reasoning tasks associated with equilibrium logic and nested logic programs into quantified propositional logic, an extension of classical propositional logic where quantifications over atomic formulas are permitted. We provide reductions not only for decision problems, but also for the central semantical concepts of equilibrium logic and nested logic programs. In particular, our encodings map a given decision problem into some formula such that the latter is valid precisely in case the former holds. The basic tasks we deal with here are the consistency problem, brave reasoning, and skeptical reasoning. Additionally, we also provide encodings for testing equivalence of theories or programs under different notions of equivalence, viz. ordinary, strong, and uniform equivalence. For all considered reasoning tasks, we analyse their computational complexity and give strict complexity bounds.