Logical Foundations of RDF(S) with Datatypes

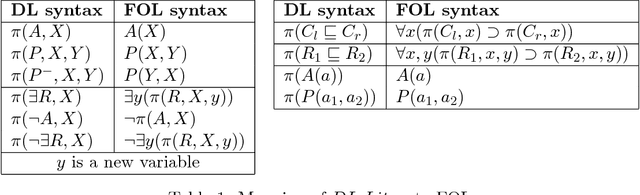
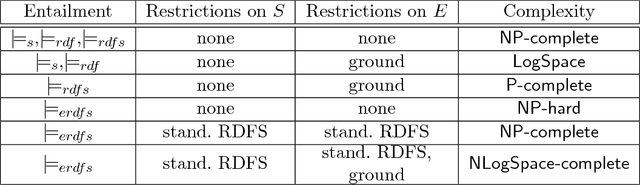
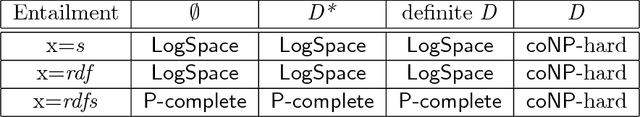
The Resource Description Framework (RDF) is a Semantic Web standard that provides a data language, simply called RDF, as well as a lightweight ontology language, called RDF Schema. We investigate embeddings of RDF in logic and show how standard logic programming and description logic technology can be used for reasoning with RDF. We subsequently consider extensions of RDF with datatype support, considering D entailment, defined in the RDF semantics specification, and D* entailment, a semantic weakening of D entailment, introduced by ter Horst. We use the embeddings and properties of the logics to establish novel upper bounds for the complexity of deciding entailment. We subsequently establish two novel lower bounds, establishing that RDFS entailment is PTime-complete and that simple-D entailment is coNP-hard, when considering arbitrary datatypes, both in the size of the entailing graph. The results indicate that RDFS may not be as lightweight as one may expect.

Embedding Non-Ground Logic Programs into Autoepistemic Logic for Knowledge Base Combination

In the context of the Semantic Web, several approaches to the combination of ontologies, given in terms of theories of classical first-order logic and rule bases, have been proposed. They either cast rules into classical logic or limit the interaction between rules and ontologies. Autoepistemic logic (AEL) is an attractive formalism which allows to overcome these limitations, by serving as a uniform host language to embed ontologies and nonmonotonic logic programs into it. For the latter, so far only the propositional setting has been considered. In this paper, we present three embeddings of normal and three embeddings of disjunctive non-ground logic programs under the stable model semantics into first-order AEL. While the embeddings all correspond with respect to objective ground atoms, differences arise when considering non-atomic formulas and combinations with first-order theories. We compare the embeddings with respect to stable expansions and autoepistemic consequences, considering the embeddings by themselves, as well as combinations with classical theories. Our results reveal differences and correspondences of the embeddings and provide useful guidance in the choice of a particular embedding for knowledge combination.