Logical Foundations of RDF(S) with Datatypes

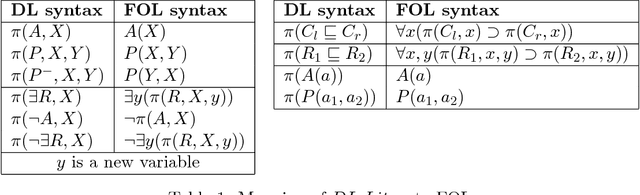
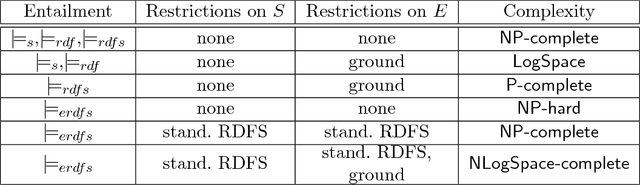
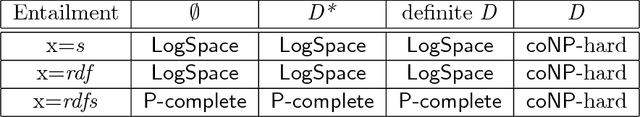
The Resource Description Framework (RDF) is a Semantic Web standard that provides a data language, simply called RDF, as well as a lightweight ontology language, called RDF Schema. We investigate embeddings of RDF in logic and show how standard logic programming and description logic technology can be used for reasoning with RDF. We subsequently consider extensions of RDF with datatype support, considering D entailment, defined in the RDF semantics specification, and D* entailment, a semantic weakening of D entailment, introduced by ter Horst. We use the embeddings and properties of the logics to establish novel upper bounds for the complexity of deciding entailment. We subsequently establish two novel lower bounds, establishing that RDFS entailment is PTime-complete and that simple-D entailment is coNP-hard, when considering arbitrary datatypes, both in the size of the entailing graph. The results indicate that RDFS may not be as lightweight as one may expect.

Query Answering in Object Oriented Knowledge Bases in Logic Programming: Description and Challenge for ASP

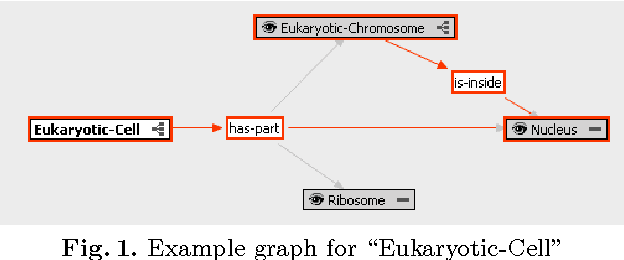
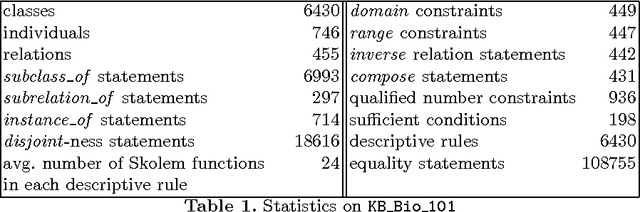
Research on developing efficient and scalable ASP solvers can substantially benefit by the availability of data sets to experiment with. KB_Bio_101 contains knowledge from a biology textbook, has been developed as part of Project Halo, and has recently become available for research use. KB_Bio_101 is one of the largest KBs available in ASP and the reasoning with it is undecidable in general. We give a description of this KB and ASP programs for a suite of queries that have been of practical interest. We explain why these queries pose significant practical challenges for the current ASP solvers.

Open Answer Set Programming with Guarded Programs

Open answer set programming (OASP) is an extension of answer set programming where one may ground a program with an arbitrary superset of the program's constants. We define a fixed point logic (FPL) extension of Clark's completion such that open answer sets correspond to models of FPL formulas and identify a syntactic subclass of programs, called (loosely) guarded programs. Whereas reasoning with general programs in OASP is undecidable, the FPL translation of (loosely) guarded programs falls in the decidable (loosely) guarded fixed point logic (mu(L)GF). Moreover, we reduce normal closed ASP to loosely guarded OASP, enabling for the first time, a characterization of an answer set semantics by muLGF formulas. We further extend the open answer set semantics for programs with generalized literals. Such generalized programs (gPs) have interesting properties, e.g., the ability to express infinity axioms. We restrict the syntax of gPs such that both rules and generalized literals are guarded. Via a translation to guarded fixed point logic, we deduce 2-exptime-completeness of satisfiability checking in such guarded gPs (GgPs). Bound GgPs are restricted GgPs with exptime-complete satisfiability checking, but still sufficiently expressive to optimally simulate computation tree logic (CTL). We translate Datalog lite programs to GgPs, establishing equivalence of GgPs under an open answer set semantics, alternation-free muGF, and Datalog lite.