Expert Selection in Distributed Gaussian Processes: A Multi-label Classification Approach

By distributing the training process, local approximation reduces the cost of the standard Gaussian Process. An ensemble technique combines local predictions from Gaussian experts trained on different partitions of the data by assuming a perfect diversity of local predictors. Although it keeps the aggregation tractable, this assumption is often violated in practice. Taking dependencies between experts enables ensemble methods to provide consistent results. However, they have a high computational cost, which is cubic in the number of experts involved. By implementing an expert selection strategy, the final aggregation step uses fewer experts and is more efficient. Indeed, a static selection approach that assigns a fixed set of experts to each new data point cannot encode the specific properties of each unique data point. This paper proposes a flexible expert selection approach based on the characteristics of entry data points. To this end, we investigate the selection task as a multi-label classification problem where the experts define labels, and each entry point is assigned to some experts. The proposed solution's prediction quality, efficiency, and asymptotic properties are discussed in detail. We demonstrate the efficacy of our method through extensive numerical experiments using synthetic and real-world data sets.

Gaussian Graphical Models as an Ensemble Method for Distributed Gaussian Processes

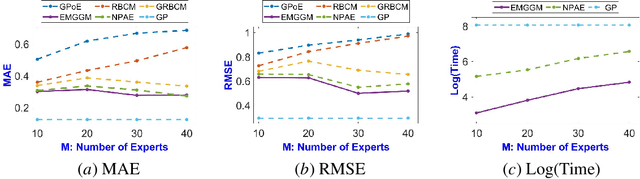
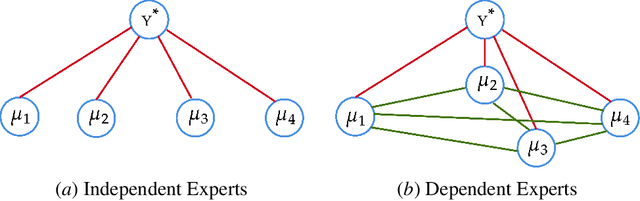
Distributed Gaussian process (DGP) is a popular approach to scale GP to big data which divides the training data into some subsets, performs local inference for each partition, and aggregates the results to acquire global prediction. To combine the local predictions, the conditional independence assumption is used which basically means there is a perfect diversity between the subsets. Although it keeps the aggregation tractable, it is often violated in practice and generally yields poor results. In this paper, we propose a novel approach for aggregating the Gaussian experts' predictions by Gaussian graphical model (GGM) where the target aggregation is defined as an unobserved latent variable and the local predictions are the observed variables. We first estimate the joint distribution of latent and observed variables using the Expectation-Maximization (EM) algorithm. The interaction between experts can be encoded by the precision matrix of the joint distribution and the aggregated predictions are obtained based on the property of conditional Gaussian distribution. Using both synthetic and real datasets, our experimental evaluations illustrate that our new method outperforms other state-of-the-art DGP approaches.

A Robust Unsupervised Ensemble of Feature-Based Explanations using Restricted Boltzmann Machines

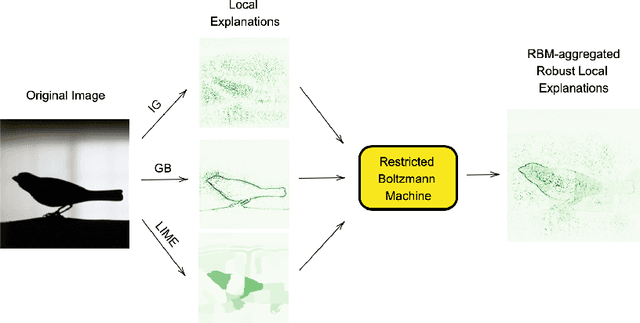
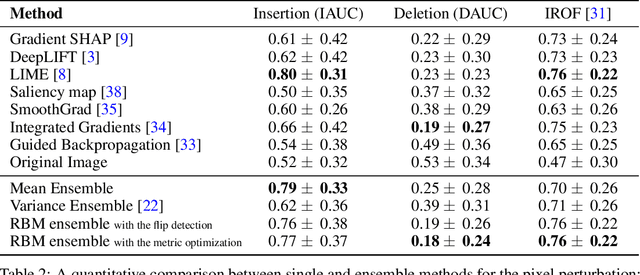
Understanding the results of deep neural networks is an essential step towards wider acceptance of deep learning algorithms. Many approaches address the issue of interpreting artificial neural networks, but often provide divergent explanations. Moreover, different hyperparameters of an explanatory method can lead to conflicting interpretations. In this paper, we propose a technique for aggregating the feature attributions of different explanatory algorithms using Restricted Boltzmann Machines (RBMs) to achieve a more reliable and robust interpretation of deep neural networks. Several challenging experiments on real-world datasets show that the proposed RBM method outperforms popular feature attribution methods and basic ensemble techniques.

Gaussian Experts Selection using Graphical Models

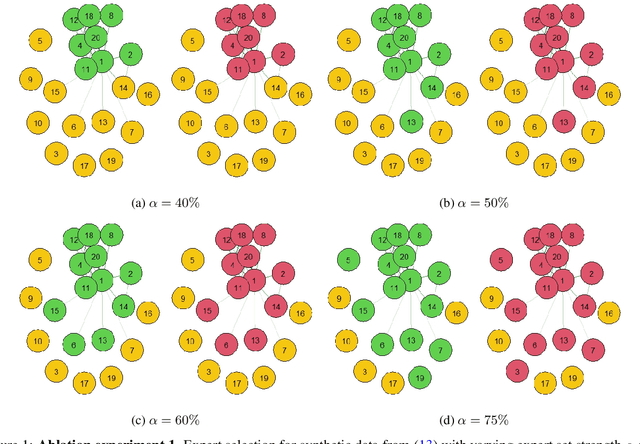
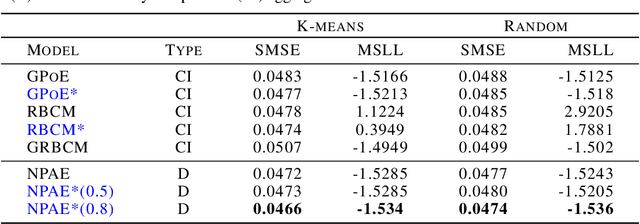
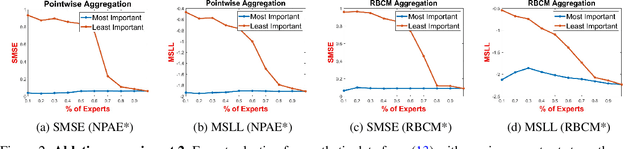
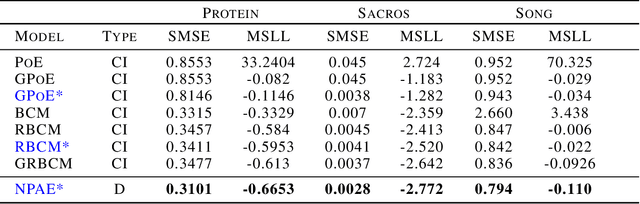
Local approximations are popular methods to scale Gaussian processes (GPs) to big data. Local approximations reduce time complexity by dividing the original dataset into subsets and training a local expert on each subset. Aggregating the experts' prediction is done assuming either conditional dependence or independence between the experts. Imposing the \emph{conditional independence assumption} (CI) between the experts renders the aggregation of different expert predictions time efficient at the cost of poor uncertainty quantification. On the other hand, modeling dependent experts can provide precise predictions and uncertainty quantification at the expense of impractically high computational costs. By eliminating weak experts via a theory-guided expert selection step, we substantially reduce the computational cost of aggregating dependent experts while ensuring calibrated uncertainty quantification. We leverage techniques from the literature on undirected graphical models, using sparse precision matrices that encode conditional dependencies between experts to select the most important experts. Moreov

Aggregating Dependent Gaussian Experts in Local Approximation

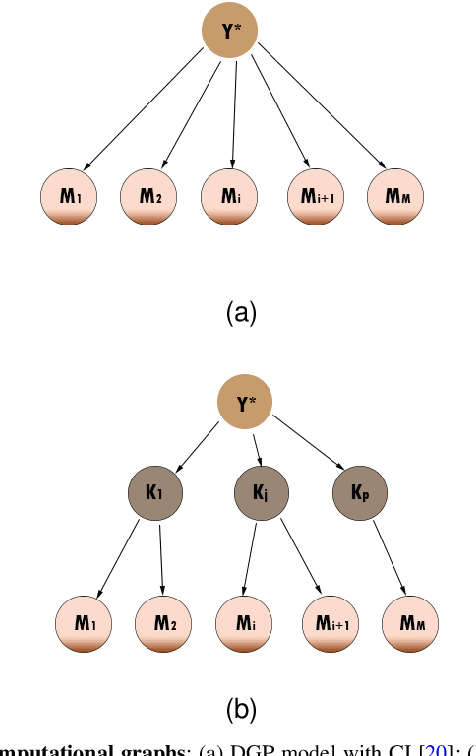
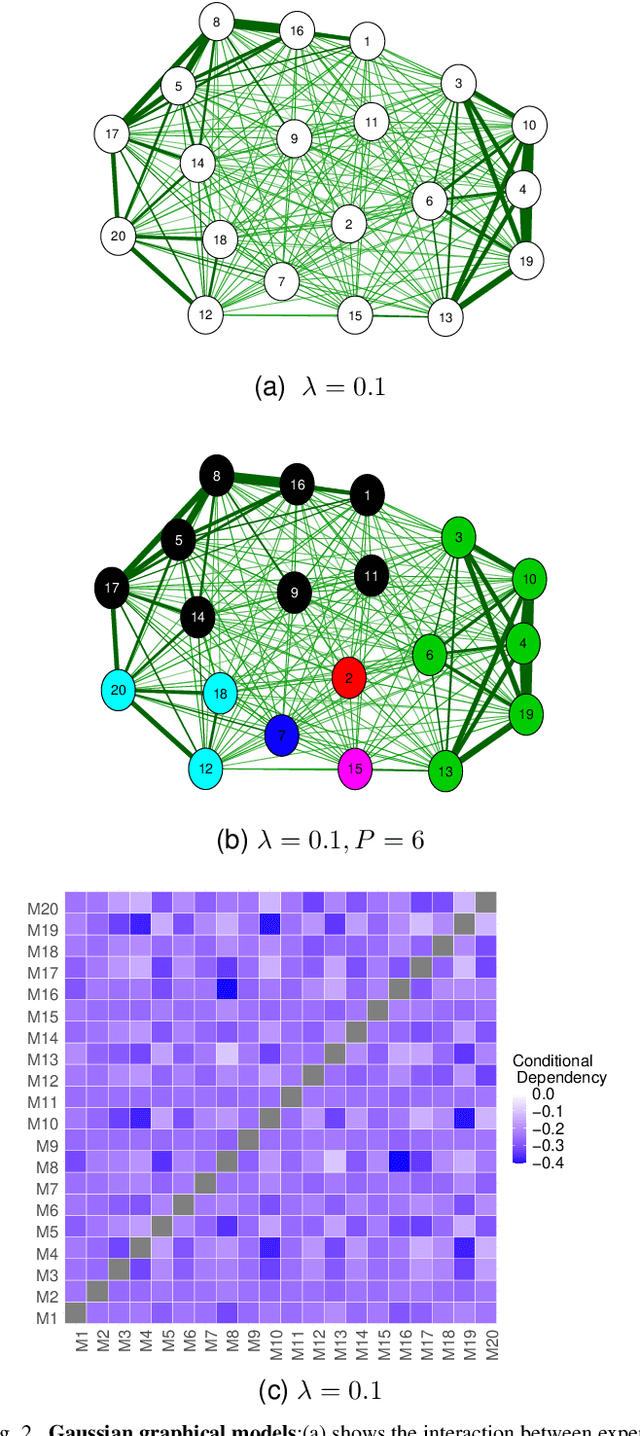
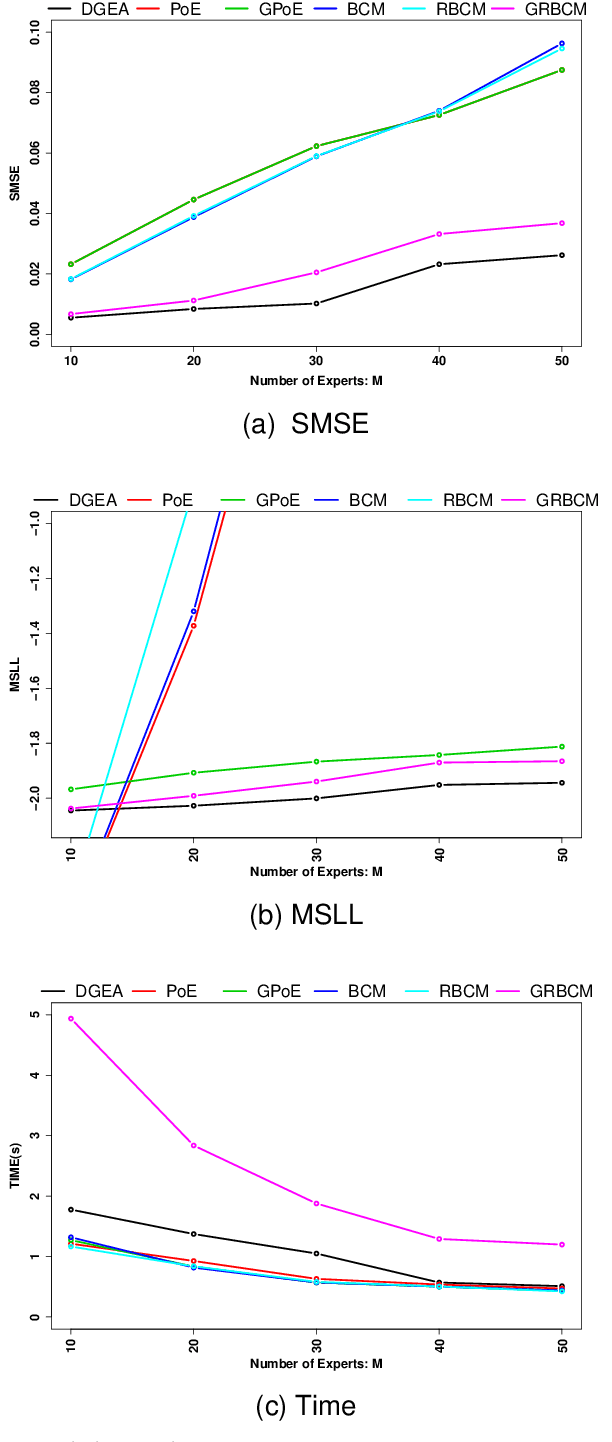
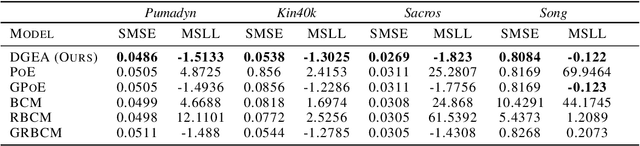
Distributed Gaussian processes (DGPs) are prominent local approximation methods to scale Gaussian processes (GPs) to large datasets. Instead of a global estimation, they train local experts by dividing the training set into subsets, thus reducing the time complexity. This strategy is based on the conditional independence assumption, which basically means that there is a perfect diversity between the local experts. In practice, however, this assumption is often violated, and the aggregation of experts leads to sub-optimal and inconsistent solutions. In this paper, we propose a novel approach for aggregating the Gaussian experts by detecting strong violations of conditional independence. The dependency between experts is determined by using a Gaussian graphical model, which yields the precision matrix. The precision matrix encodes conditional dependencies between experts and is used to detect strongly dependent experts and construct an improved aggregation. Using both synthetic and real datasets, our experimental evaluations illustrate that our new method outperforms other state-of-the-art (SOTA) DGP approaches while being substantially more time-efficient than SOTA approaches, which build on independent experts.