Gaussian Experts Selection using Graphical Models
Paper and Code
Feb 04, 2021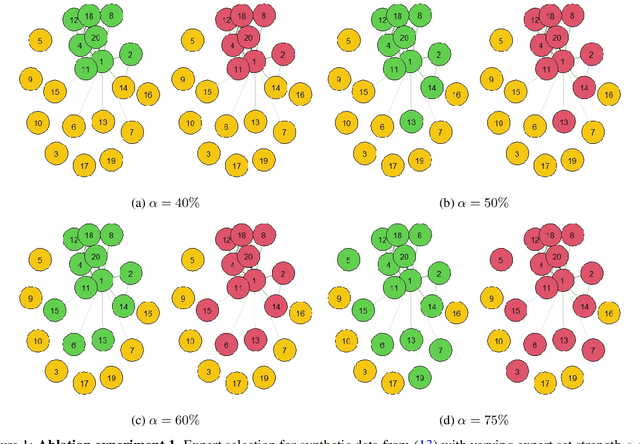
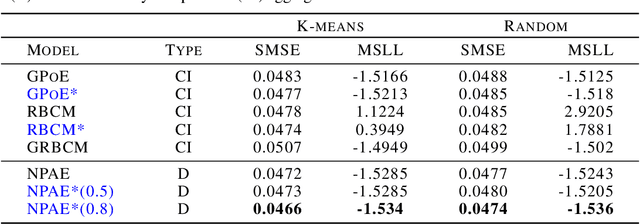
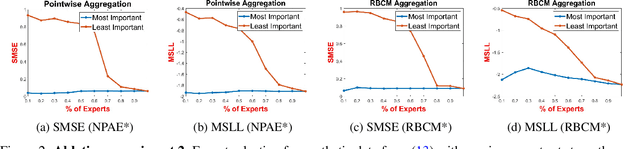
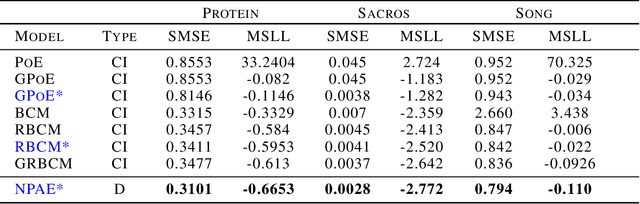
Local approximations are popular methods to scale Gaussian processes (GPs) to big data. Local approximations reduce time complexity by dividing the original dataset into subsets and training a local expert on each subset. Aggregating the experts' prediction is done assuming either conditional dependence or independence between the experts. Imposing the \emph{conditional independence assumption} (CI) between the experts renders the aggregation of different expert predictions time efficient at the cost of poor uncertainty quantification. On the other hand, modeling dependent experts can provide precise predictions and uncertainty quantification at the expense of impractically high computational costs. By eliminating weak experts via a theory-guided expert selection step, we substantially reduce the computational cost of aggregating dependent experts while ensuring calibrated uncertainty quantification. We leverage techniques from the literature on undirected graphical models, using sparse precision matrices that encode conditional dependencies between experts to select the most important experts. Moreov
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge