Implicit Data Augmentation Using Feature Interpolation for Diversified Low-Shot Image Generation

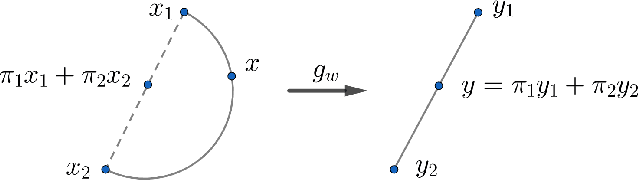
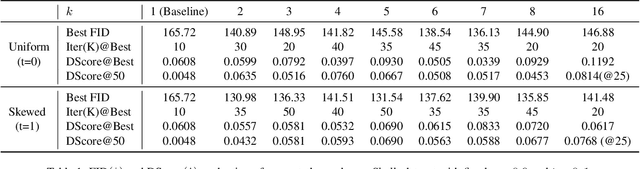
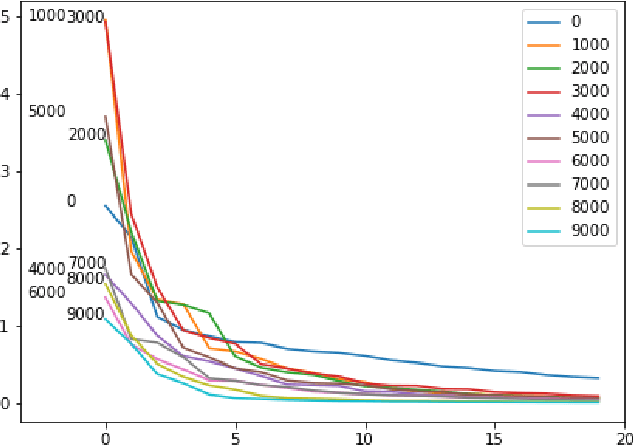
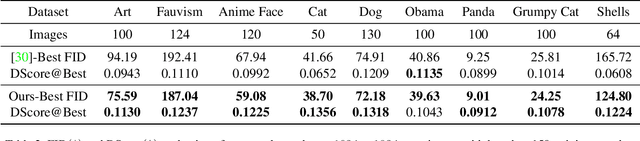
Training of generative models especially Generative Adversarial Networks can easily diverge in low-data setting. To mitigate this issue, we propose a novel implicit data augmentation approach which facilitates stable training and synthesize diverse samples. Specifically, we view the discriminator as a metric embedding of the real data manifold, which offers proper distances between real data points. We then utilize information in the feature space to develop a data-driven augmentation method. We further bring up a simple metric to evaluate the diversity of synthesized samples. Experiments on few-shot generation tasks show our method improves FID and diversity of results compared to current methods, and allows generating high-quality and diverse images with less than 100 training samples.

AWGAN: Empowering High-Dimensional Discriminator Output for Generative Adversarial Networks

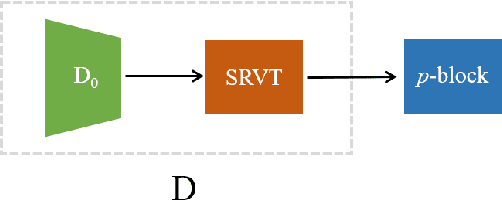
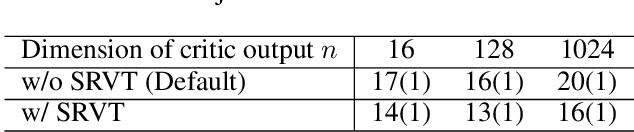
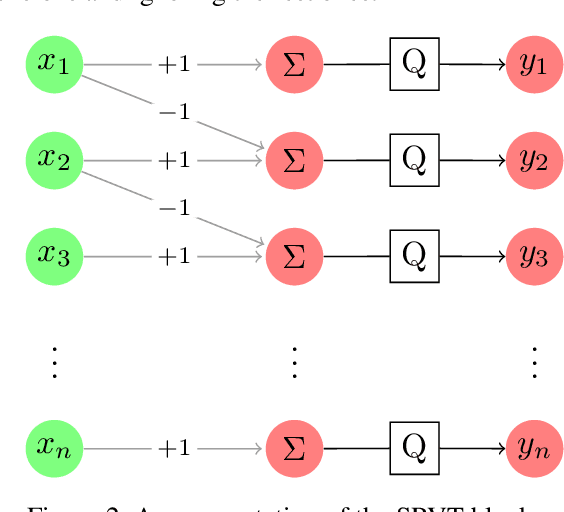
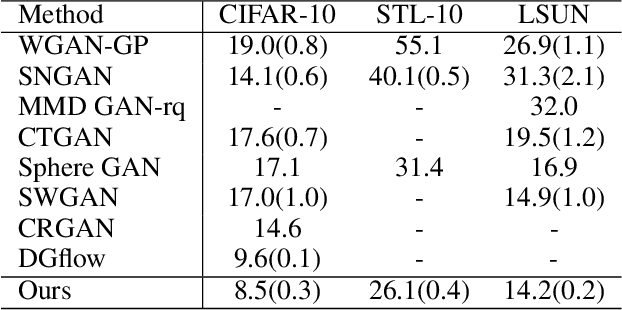
Empirically multidimensional discriminator (critic) output can be advantageous, while a solid explanation for it has not been discussed. In this paper, (i) we rigorously prove that high-dimensional critic output has advantage on distinguishing real and fake distributions; (ii) we also introduce an square-root velocity transformation (SRVT) block which further magnifies this advantage. The proof is based on our proposed maximal p-centrality discrepancy which is bounded above by p-Wasserstein distance and perfectly fits the Wasserstein GAN framework with high-dimensional critic output n. We have also showed when n = 1, the proposed discrepancy is equivalent to 1-Wasserstein distance. The SRVT block is applied to break the symmetric structure of high-dimensional critic output and improve the generalization capability of the discriminator network. In terms of implementation, the proposed framework does not require additional hyper-parameter tuning, which largely facilitates its usage. Experiments on image generation tasks show performance improvement on benchmark datasets.

Adversarial Manifold Matching via Deep Metric Learning for Generative Modeling

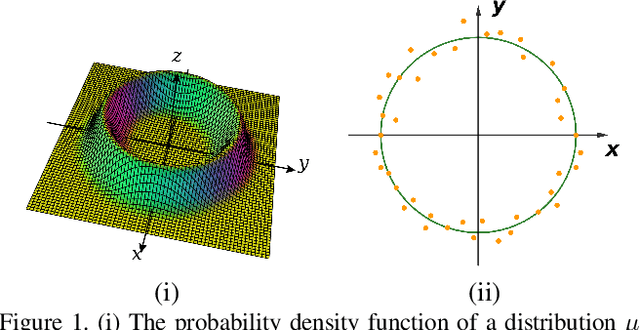
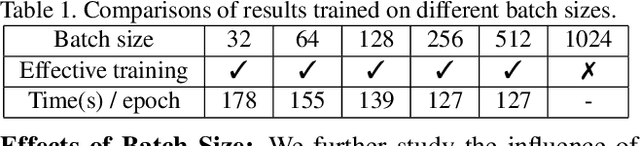
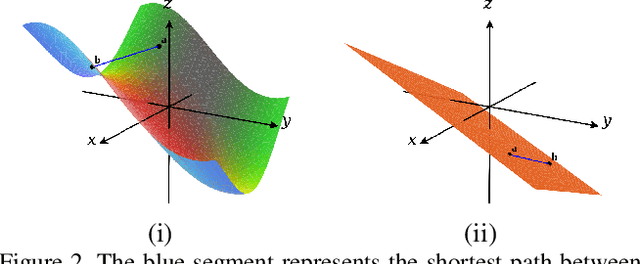
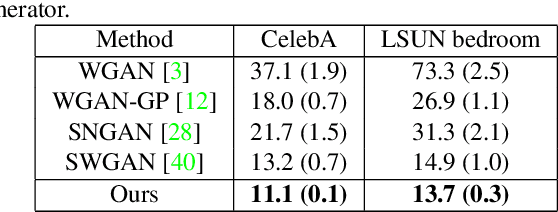
We propose a manifold matching approach to generative models which includes a distribution generator (or data generator) and a metric generator. In our framework, we view the real data set as some manifold embedded in a high-dimensional Euclidean space. The distribution generator aims at generating samples that follow some distribution condensed around the real data manifold. It is achieved by matching two sets of points using their geometric shape descriptors, such as centroid and $p$-diameter, with learned distance metric; the metric generator utilizes both real data and generated samples to learn a distance metric which is close to some intrinsic geodesic distance on the real data manifold. The produced distance metric is further used for manifold matching. The two networks are learned simultaneously during the training process. We apply the approach on both unsupervised and supervised learning tasks: in unconditional image generation task, the proposed method obtains competitive results compared with existing generative models; in super-resolution task, we incorporate the framework in perception-based models and improve visual qualities by producing samples with more natural textures. Both theoretical analysis and real data experiments guarantee the feasibility and effectiveness of the proposed framework.