AWGAN: Empowering High-Dimensional Discriminator Output for Generative Adversarial Networks

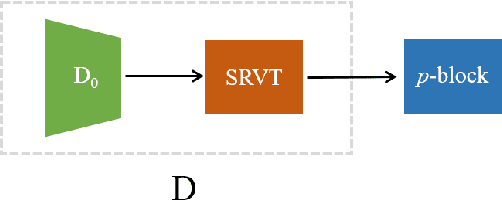
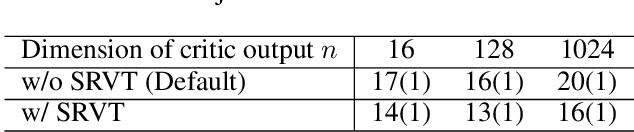
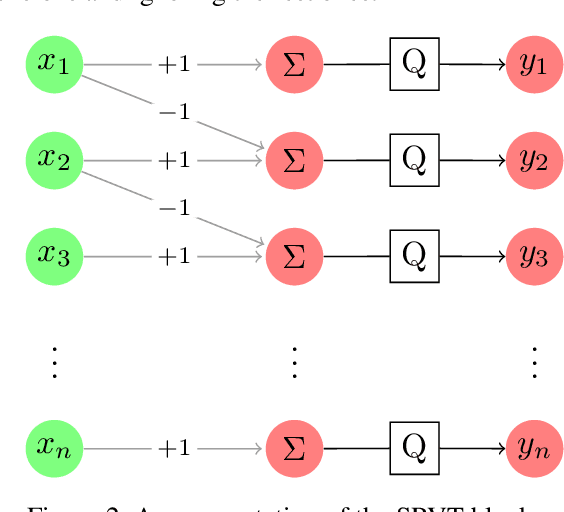
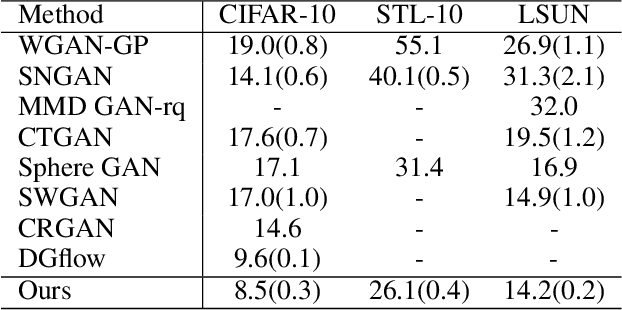
Empirically multidimensional discriminator (critic) output can be advantageous, while a solid explanation for it has not been discussed. In this paper, (i) we rigorously prove that high-dimensional critic output has advantage on distinguishing real and fake distributions; (ii) we also introduce an square-root velocity transformation (SRVT) block which further magnifies this advantage. The proof is based on our proposed maximal p-centrality discrepancy which is bounded above by p-Wasserstein distance and perfectly fits the Wasserstein GAN framework with high-dimensional critic output n. We have also showed when n = 1, the proposed discrepancy is equivalent to 1-Wasserstein distance. The SRVT block is applied to break the symmetric structure of high-dimensional critic output and improve the generalization capability of the discriminator network. In terms of implementation, the proposed framework does not require additional hyper-parameter tuning, which largely facilitates its usage. Experiments on image generation tasks show performance improvement on benchmark datasets.