Adversarial Manifold Matching via Deep Metric Learning for Generative Modeling

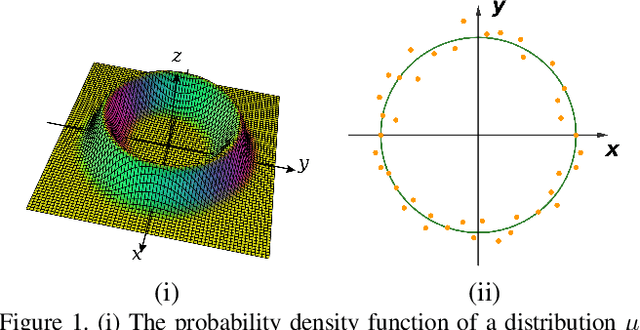
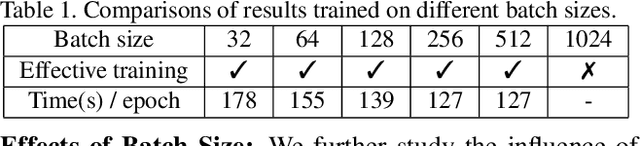
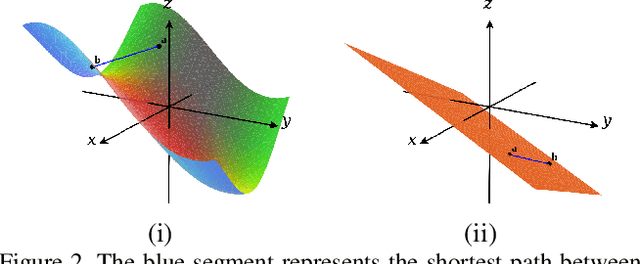
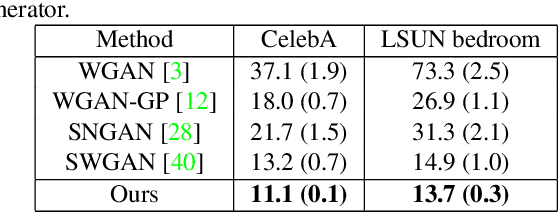
We propose a manifold matching approach to generative models which includes a distribution generator (or data generator) and a metric generator. In our framework, we view the real data set as some manifold embedded in a high-dimensional Euclidean space. The distribution generator aims at generating samples that follow some distribution condensed around the real data manifold. It is achieved by matching two sets of points using their geometric shape descriptors, such as centroid and $p$-diameter, with learned distance metric; the metric generator utilizes both real data and generated samples to learn a distance metric which is close to some intrinsic geodesic distance on the real data manifold. The produced distance metric is further used for manifold matching. The two networks are learned simultaneously during the training process. We apply the approach on both unsupervised and supervised learning tasks: in unconditional image generation task, the proposed method obtains competitive results compared with existing generative models; in super-resolution task, we incorporate the framework in perception-based models and improve visual qualities by producing samples with more natural textures. Both theoretical analysis and real data experiments guarantee the feasibility and effectiveness of the proposed framework.