On Circuit Depth Scaling For Quantum Approximate Optimization

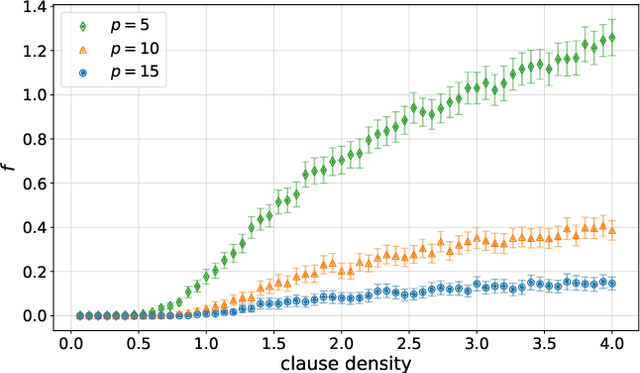
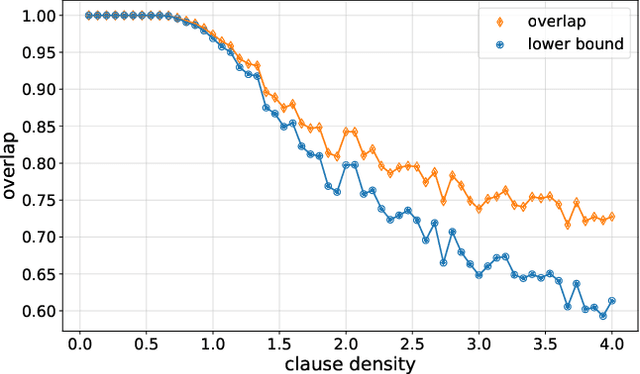
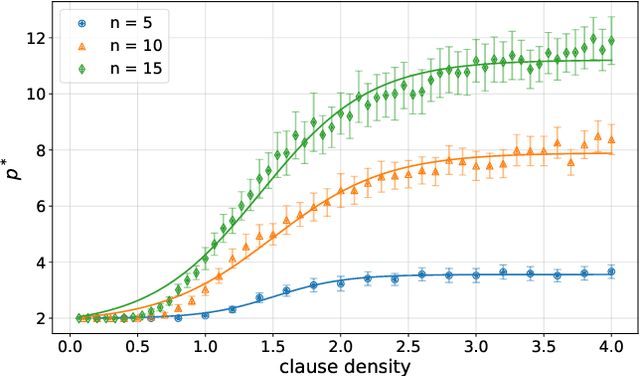
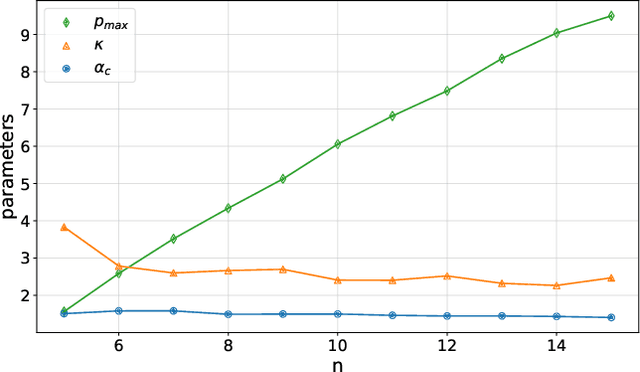
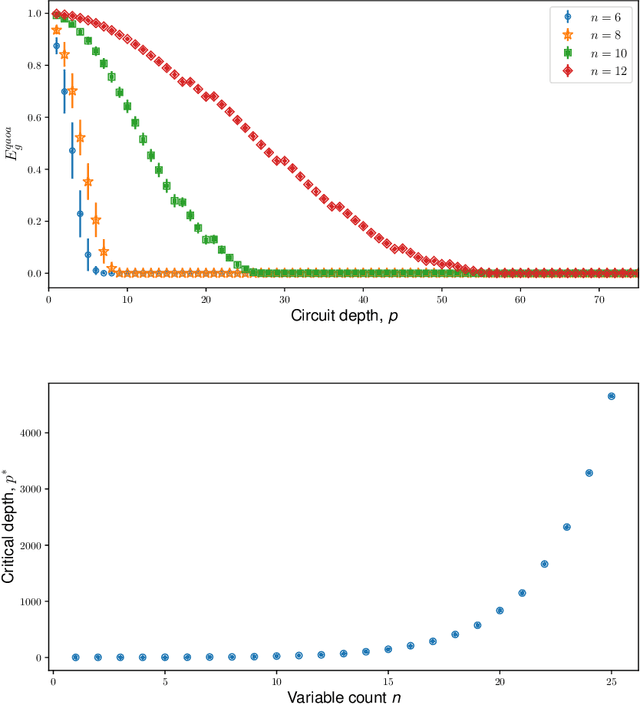
Variational quantum algorithms are the centerpiece of modern quantum programming. These algorithms involve training parameterized quantum circuits using a classical co-processor, an approach adapted partly from classical machine learning. An important subclass of these algorithms, designed for combinatorial optimization on currrent quantum hardware, is the quantum approximate optimization algorithm (QAOA). It is known that problem density - a problem constraint to variable ratio - induces under-parametrization in fixed depth QAOA. Density dependent performance has been reported in the literature, yet the circuit depth required to achieve fixed performance (henceforth called critical depth) remained unknown. Here, we propose a predictive model, based on a logistic saturation conjecture for critical depth scaling with respect to density. Focusing on random instances of MAX-2-SAT, we test our predictive model against simulated data with up to 15 qubits. We report the average critical depth, required to attain a success probability of 0.7, saturates at a value of 10 for densities beyond 4. We observe the predictive model to describe the simulated data within a $3\sigma$ confidence interval. Furthermore, based on the model, a linear trend for the critical depth with respect problem size is recovered for the range of 5 to 15 qubits.

Reachability Deficits in Quantum Approximate Optimization

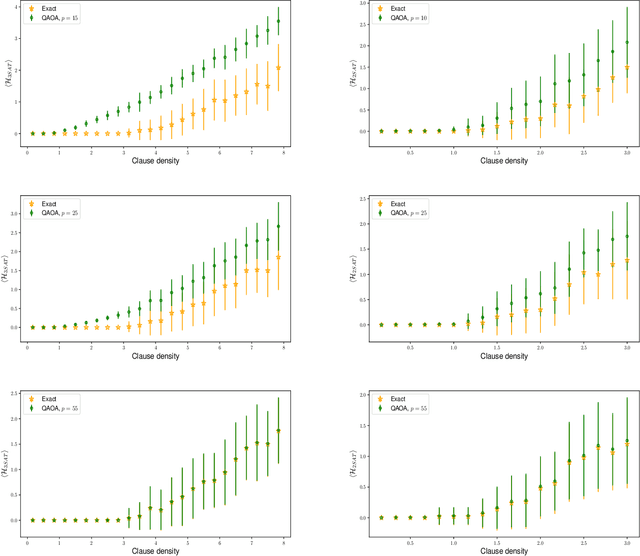
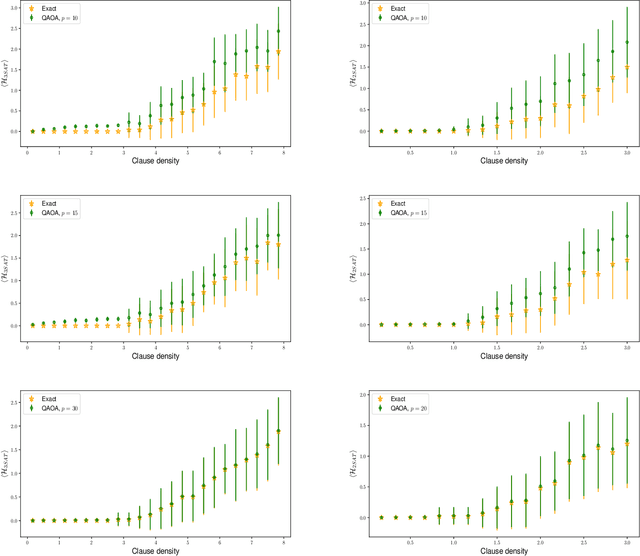
The quantum approximate optimization algorithm (QAOA) has rapidly become a cornerstone of contemporary quantum algorithm development. Despite a growing range of applications, only a few results have been developed towards understanding the algorithms ultimate limitations. Here we report that QAOA exhibits a strong dependence on a problem instances constraint to variable ratio - this problem density places a limiting restriction on the algorithms capacity to minimize a corresponding objective function (and hence solve optimization problems). Such 'reachability deficits' persist even in the absence of barren plateaus [McClean et al., 2018] and are outside of the recently reported level-1 QAOA limitations [Hastings 2019]. Building on general numerical experiments, we compare the presence of reachability deficits with analytic solutions of the variational model of Grover's search algorithm.

Computational Phase Transition Signature in Gibbs Sampling

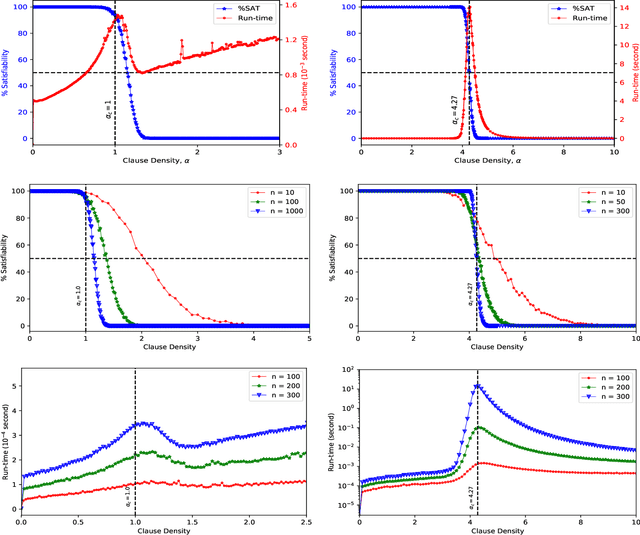
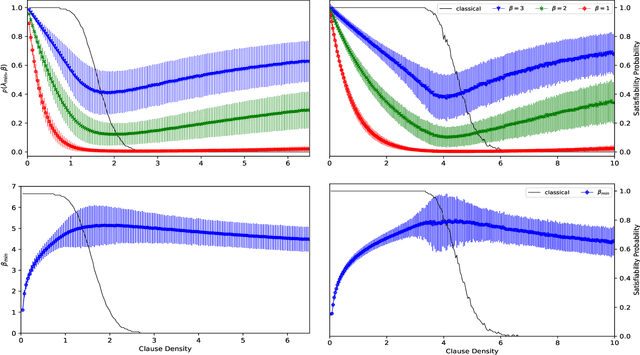
Gibbs sampling is fundamental to a wide range of computer algorithms. Such algorithms are set to be replaced by physics based processors$-$be it quantum or stochastic annealing devices$-$which embed problem instances and evolve a physical system into an ensemble to recover a probability distribution. At a critical constraint to variable ratio, decision problems$-$such as propositional satisfiability$-$appear to statistically exhibit an abrupt transition in required computational resources. This so called, algorithmic or computational phase transition signature, has yet-to-be observed in contemporary physics based processors. We found that the computational phase transition admits a signature in Gibbs' distributions and hence we predict and prescribe the physical observation of this effect. We simulate such an experiment, that when realized experimentally, we believe would represent a milestone in the physical theory of computation.