Computational Phase Transition Signature in Gibbs Sampling
Paper and Code
Jun 25, 2019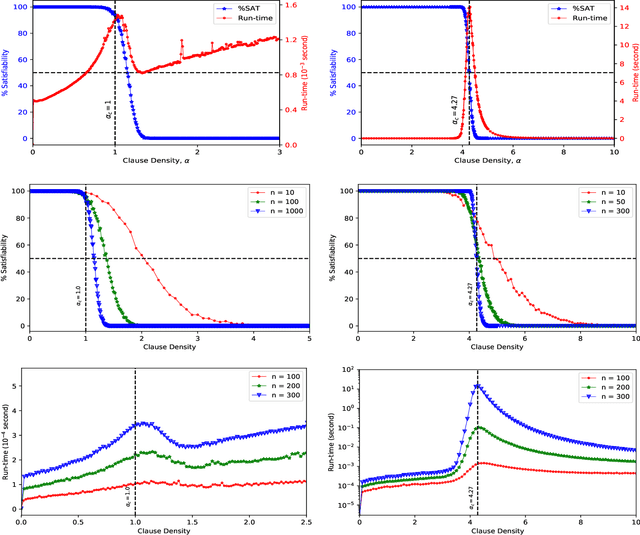
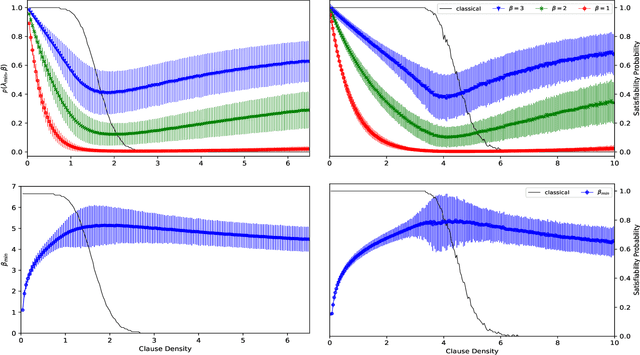
Gibbs sampling is fundamental to a wide range of computer algorithms. Such algorithms are set to be replaced by physics based processors$-$be it quantum or stochastic annealing devices$-$which embed problem instances and evolve a physical system into an ensemble to recover a probability distribution. At a critical constraint to variable ratio, decision problems$-$such as propositional satisfiability$-$appear to statistically exhibit an abrupt transition in required computational resources. This so called, algorithmic or computational phase transition signature, has yet-to-be observed in contemporary physics based processors. We found that the computational phase transition admits a signature in Gibbs' distributions and hence we predict and prescribe the physical observation of this effect. We simulate such an experiment, that when realized experimentally, we believe would represent a milestone in the physical theory of computation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge