On Circuit Depth Scaling For Quantum Approximate Optimization

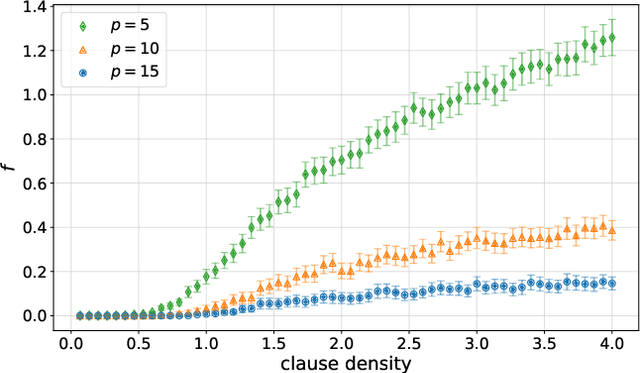
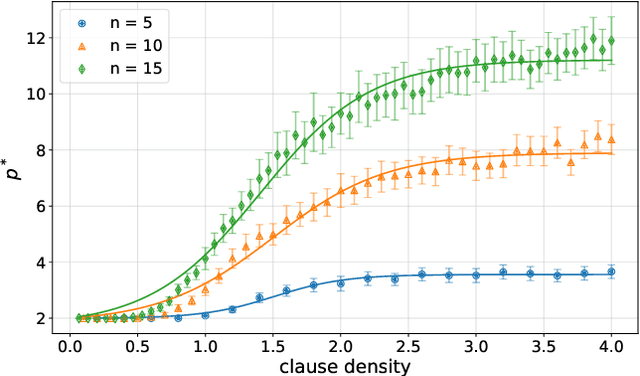
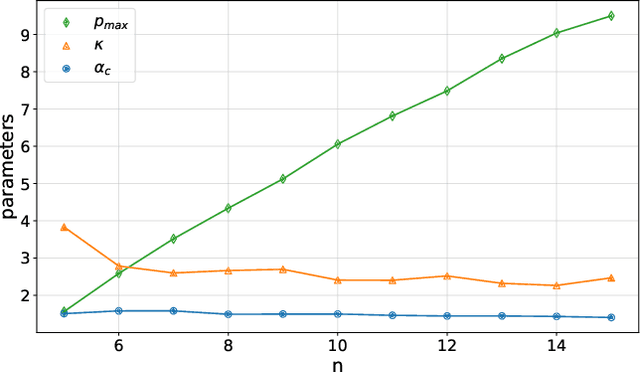
Variational quantum algorithms are the centerpiece of modern quantum programming. These algorithms involve training parameterized quantum circuits using a classical co-processor, an approach adapted partly from classical machine learning. An important subclass of these algorithms, designed for combinatorial optimization on currrent quantum hardware, is the quantum approximate optimization algorithm (QAOA). It is known that problem density - a problem constraint to variable ratio - induces under-parametrization in fixed depth QAOA. Density dependent performance has been reported in the literature, yet the circuit depth required to achieve fixed performance (henceforth called critical depth) remained unknown. Here, we propose a predictive model, based on a logistic saturation conjecture for critical depth scaling with respect to density. Focusing on random instances of MAX-2-SAT, we test our predictive model against simulated data with up to 15 qubits. We report the average critical depth, required to attain a success probability of 0.7, saturates at a value of 10 for densities beyond 4. We observe the predictive model to describe the simulated data within a $3\sigma$ confidence interval. Furthermore, based on the model, a linear trend for the critical depth with respect problem size is recovered for the range of 5 to 15 qubits.

Training Saturation in Layerwise Quantum Approximate Optimisation

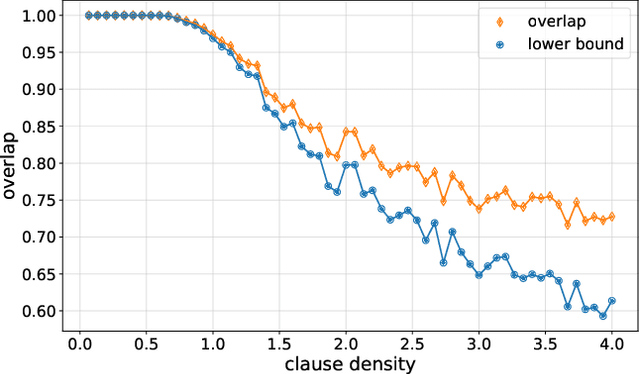
Quantum Approximate Optimisation (QAOA) is the most studied gate based variational quantum algorithm today. We train QAOA one layer at a time to maximize overlap with an $n$ qubit target state. Doing so we discovered that such training always saturates -- called \textit{training saturation} -- at some depth $p^*$, meaning that past a certain depth, overlap can not be improved by adding subsequent layers. We formulate necessary conditions for saturation. Numerically, we find layerwise QAOA reaches its maximum overlap at depth $p^*=n$. The addition of coherent dephasing errors to training removes saturation, recovering robustness to layerwise training. This study sheds new light on the performance limitations and prospects of QAOA.