Graph Neural Networks on Quantum Computers

Graph Neural Networks (GNNs) are powerful machine learning models that excel at analyzing structured data represented as graphs, demonstrating remarkable performance in applications like social network analysis and recommendation systems. However, classical GNNs face scalability challenges when dealing with large-scale graphs. This paper proposes frameworks for implementing GNNs on quantum computers to potentially address the challenges. We devise quantum algorithms corresponding to the three fundamental types of classical GNNs: Graph Convolutional Networks, Graph Attention Networks, and Message-Passing GNNs. A complexity analysis of our quantum implementation of the Simplified Graph Convolutional (SGC) Network shows potential quantum advantages over its classical counterpart, with significant improvements in time and space complexities. Our complexities can have trade-offs between the two: when optimizing for minimal circuit depth, our quantum SGC achieves logarithmic time complexity in the input sizes (albeit at the cost of linear space complexity). When optimizing for minimal qubit usage, the quantum SGC exhibits space complexity logarithmic in the input sizes, offering an exponential reduction compared to classical SGCs, while still maintaining better time complexity. These results suggest our Quantum GNN frameworks could efficiently process large-scale graphs. This work paves the way for implementing more advanced Graph Neural Network models on quantum computers, opening new possibilities in quantum machine learning for analyzing graph-structured data.

On Circuit Depth Scaling For Quantum Approximate Optimization

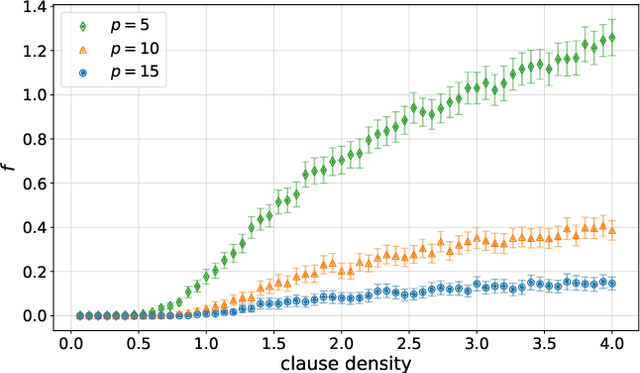
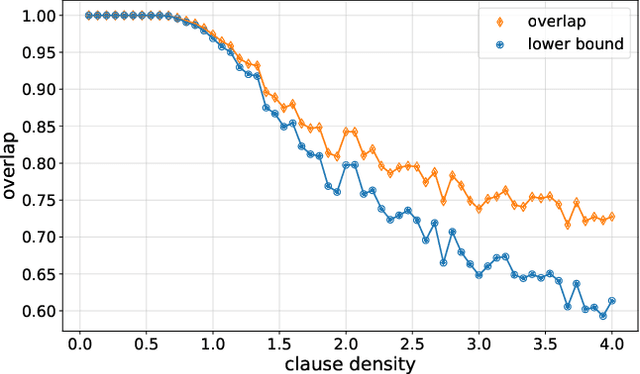
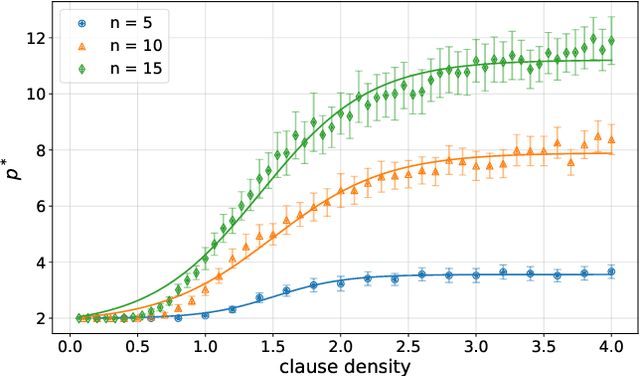
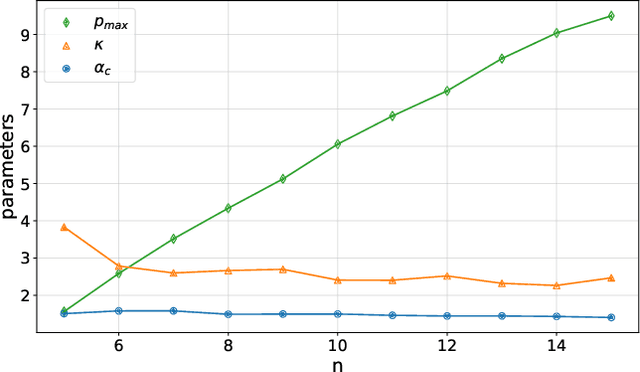
Variational quantum algorithms are the centerpiece of modern quantum programming. These algorithms involve training parameterized quantum circuits using a classical co-processor, an approach adapted partly from classical machine learning. An important subclass of these algorithms, designed for combinatorial optimization on currrent quantum hardware, is the quantum approximate optimization algorithm (QAOA). It is known that problem density - a problem constraint to variable ratio - induces under-parametrization in fixed depth QAOA. Density dependent performance has been reported in the literature, yet the circuit depth required to achieve fixed performance (henceforth called critical depth) remained unknown. Here, we propose a predictive model, based on a logistic saturation conjecture for critical depth scaling with respect to density. Focusing on random instances of MAX-2-SAT, we test our predictive model against simulated data with up to 15 qubits. We report the average critical depth, required to attain a success probability of 0.7, saturates at a value of 10 for densities beyond 4. We observe the predictive model to describe the simulated data within a $3\sigma$ confidence interval. Furthermore, based on the model, a linear trend for the critical depth with respect problem size is recovered for the range of 5 to 15 qubits.

Low-Depth Optical Neural Networks

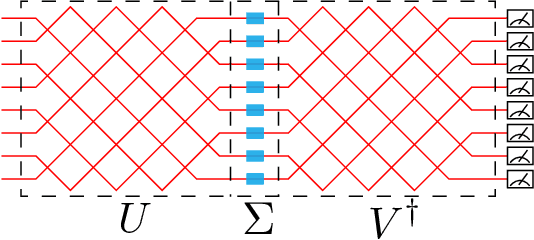
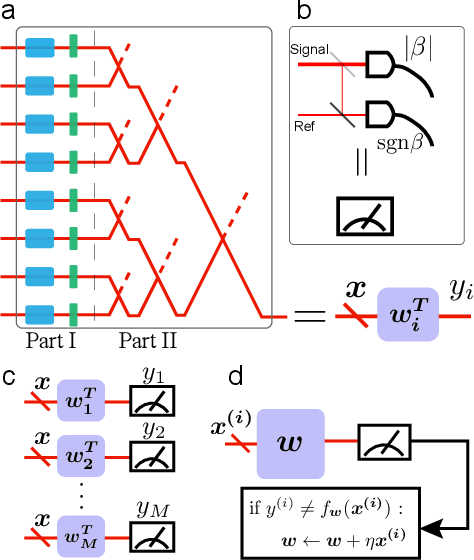
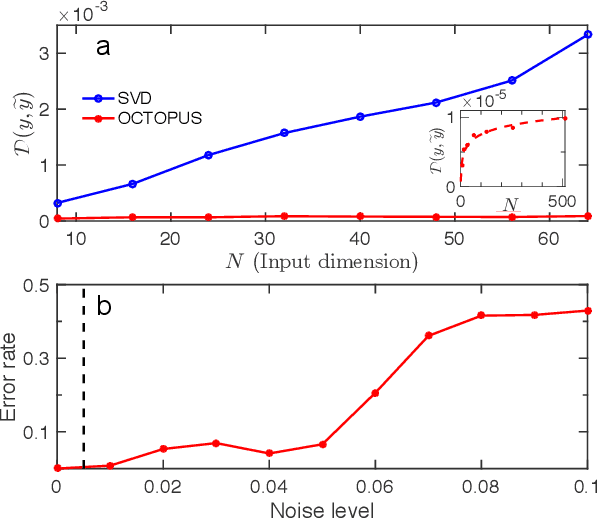
Optical neural network (ONN) is emerging as an attractive proposal for machine-learning applications, enabling high-speed computation with low-energy consumption. However, there are several challenges in applying ONN for industrial applications, including the realization of activation functions and maintaining stability. In particular, the stability of ONNs decrease with the circuit depth, limiting the scalability of the ONNs for practical uses. Here we demonstrate how to compress the circuit depth of ONN to scale only logarithmically, leading to an exponential gain in terms of noise robustness. Our low-depth (LD) ONN is based on an architecture, called Optical CompuTing Of dot-Product UnitS (OCTOPUS), which can also be applied individually as a linear perceptron for solving classification problems. Using the standard data set of Letter Recognition, we present numerical evidence showing that LD-ONN can exhibit a significant gain in noise robustness, compared with a previous ONN proposal based on singular-value decomposition [Nature Photonics 11, 441 (2017)].