On Circuit Depth Scaling For Quantum Approximate Optimization
Paper and Code
May 03, 2022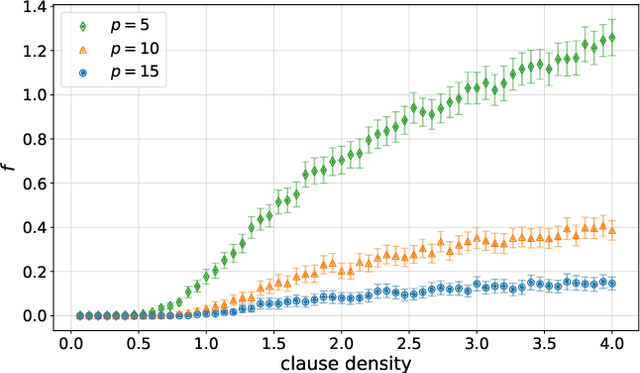
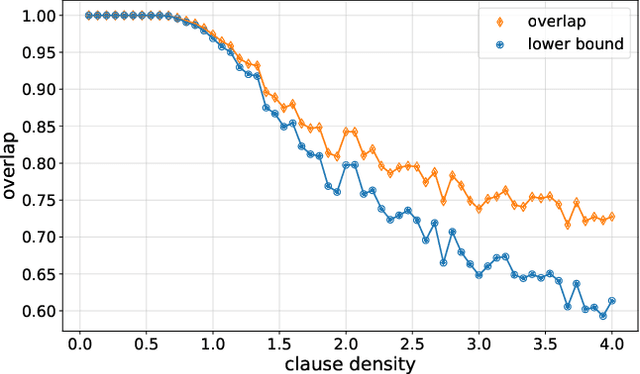
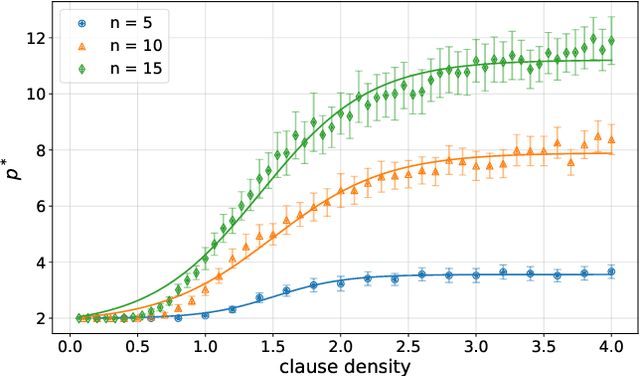
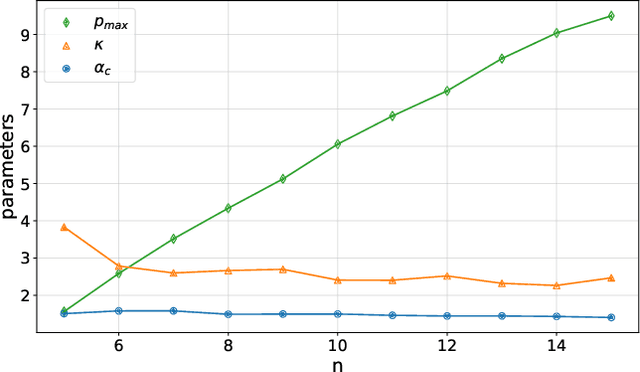
Variational quantum algorithms are the centerpiece of modern quantum programming. These algorithms involve training parameterized quantum circuits using a classical co-processor, an approach adapted partly from classical machine learning. An important subclass of these algorithms, designed for combinatorial optimization on currrent quantum hardware, is the quantum approximate optimization algorithm (QAOA). It is known that problem density - a problem constraint to variable ratio - induces under-parametrization in fixed depth QAOA. Density dependent performance has been reported in the literature, yet the circuit depth required to achieve fixed performance (henceforth called critical depth) remained unknown. Here, we propose a predictive model, based on a logistic saturation conjecture for critical depth scaling with respect to density. Focusing on random instances of MAX-2-SAT, we test our predictive model against simulated data with up to 15 qubits. We report the average critical depth, required to attain a success probability of 0.7, saturates at a value of 10 for densities beyond 4. We observe the predictive model to describe the simulated data within a $3\sigma$ confidence interval. Furthermore, based on the model, a linear trend for the critical depth with respect problem size is recovered for the range of 5 to 15 qubits.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge