Reachability Deficits in Quantum Approximate Optimization
Paper and Code
Jun 26, 2019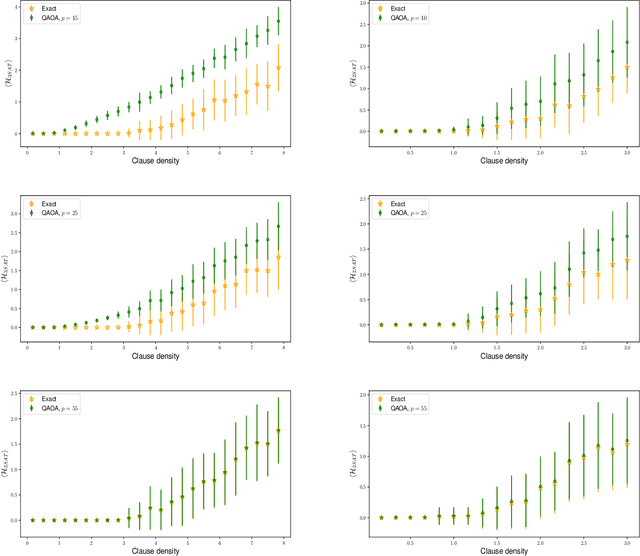
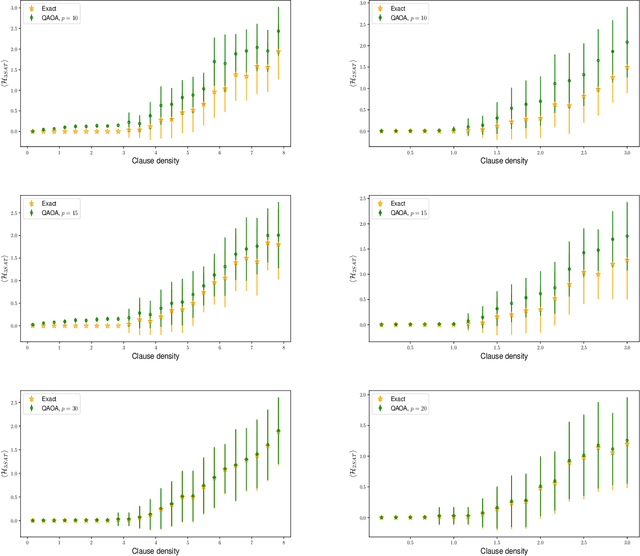
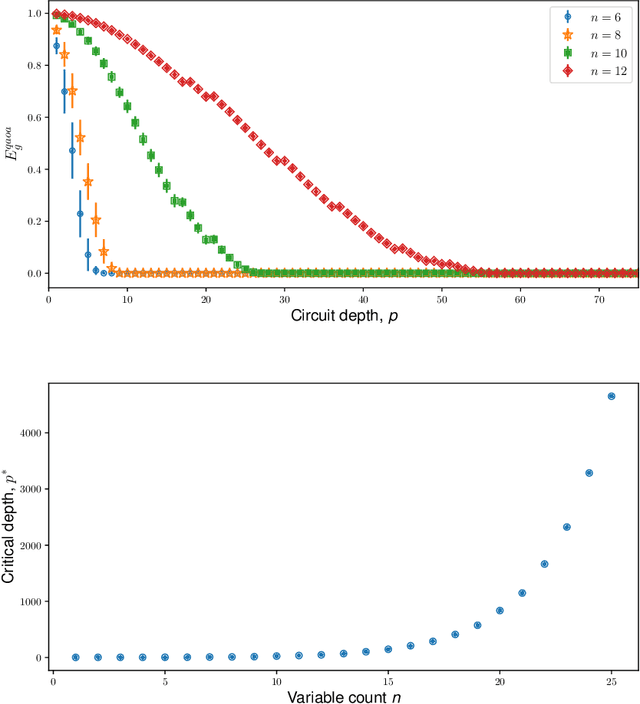
The quantum approximate optimization algorithm (QAOA) has rapidly become a cornerstone of contemporary quantum algorithm development. Despite a growing range of applications, only a few results have been developed towards understanding the algorithms ultimate limitations. Here we report that QAOA exhibits a strong dependence on a problem instances constraint to variable ratio - this problem density places a limiting restriction on the algorithms capacity to minimize a corresponding objective function (and hence solve optimization problems). Such 'reachability deficits' persist even in the absence of barren plateaus [McClean et al., 2018] and are outside of the recently reported level-1 QAOA limitations [Hastings 2019]. Building on general numerical experiments, we compare the presence of reachability deficits with analytic solutions of the variational model of Grover's search algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge