On Artificial Life and Emergent Computation in Physical Substrates

In living systems, we often see the emergence of the ingredients necessary for computation -- the capacity for information transmission, storage, and modification -- begging the question of how we may exploit or imitate such biological systems in unconventional computing applications. What can we gain from artificial life in the advancement of computing technology? Artificial life provides us with powerful tools for understanding the dynamic behavior of biological systems and capturing this behavior in manmade substrates. With this approach, we can move towards a new computing paradigm concerned with harnessing emergent computation in physical substrates not governed by the constraints of Moore's law and ultimately realize massively parallel and distributed computing technology. In this paper, we argue that the lens of artificial life offers valuable perspectives for the advancement of high-performance computing technology. We first present a brief foundational background on artificial life and some relevant tools that may be applicable to unconventional computing. Two specific substrates are then discussed in detail: biological neurons and ensembles of nanomagnets. These substrates are the focus of the authors' ongoing work, and they are illustrative of the two sides of the approach outlined here -- the close study of living systems and the construction of artificial systems to produce life-like behaviors. We conclude with a philosophical discussion on what we can learn from approaching computation with the curiosity inherent to the study of artificial life. The main contribution of this paper is to present the great potential of using artificial life methodologies to uncover and harness the inherent computational power of physical substrates toward applications in unconventional high-performance computing.

A general representation of dynamical systems for reservoir computing

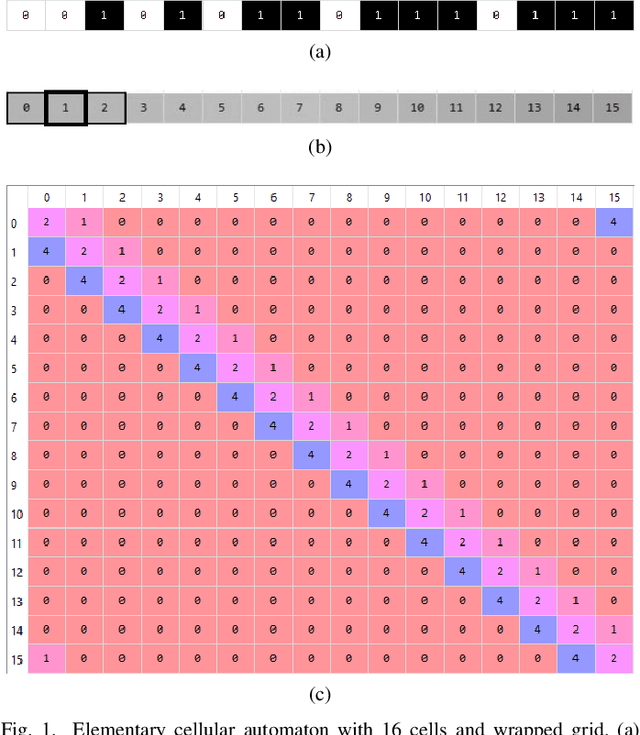
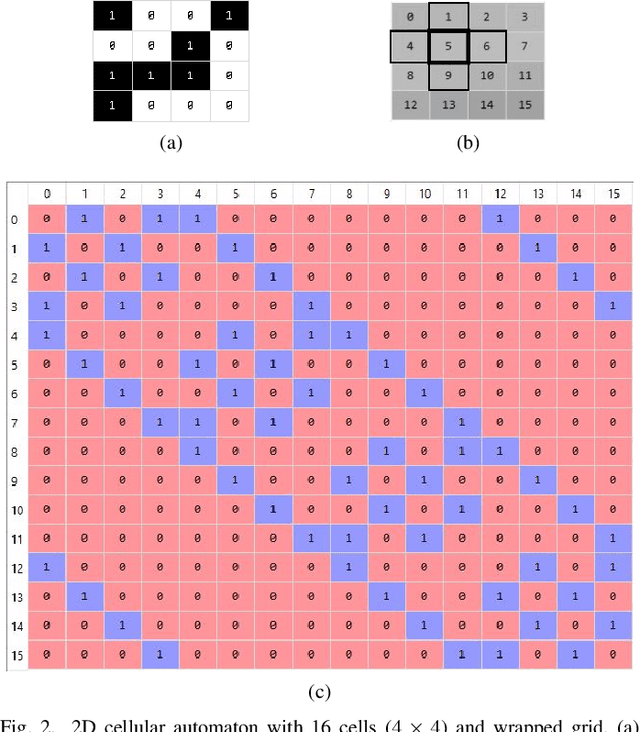
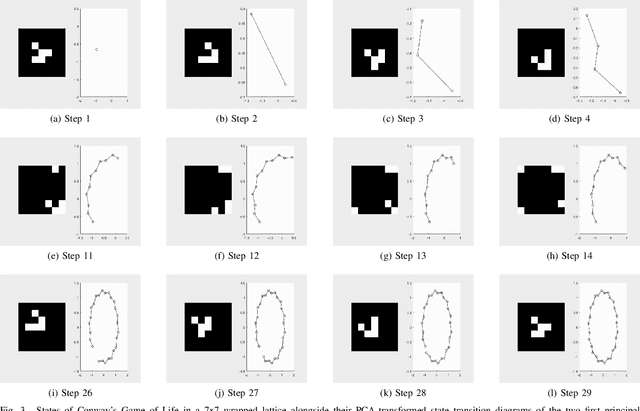
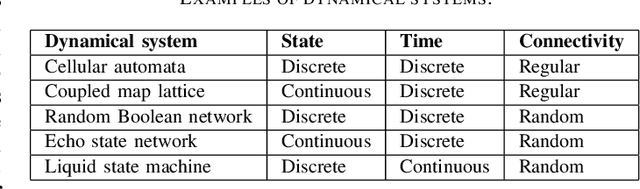
Dynamical systems are capable of performing computation in a reservoir computing paradigm. This paper presents a general representation of these systems as an artificial neural network (ANN). Initially, we implement the simplest dynamical system, a cellular automaton. The mathematical fundamentals behind an ANN are maintained, but the weights of the connections and the activation function are adjusted to work as an update rule in the context of cellular automata. The advantages of such implementation are its usage on specialized and optimized deep learning libraries, the capabilities to generalize it to other types of networks and the possibility to evolve cellular automata and other dynamical systems in terms of connectivity, update and learning rules. Our implementation of cellular automata constitutes an initial step towards a general framework for dynamical systems. It aims to evolve such systems to optimize their usage in reservoir computing and to model physical computing substrates.