A general representation of dynamical systems for reservoir computing
Paper and Code
Jul 03, 2019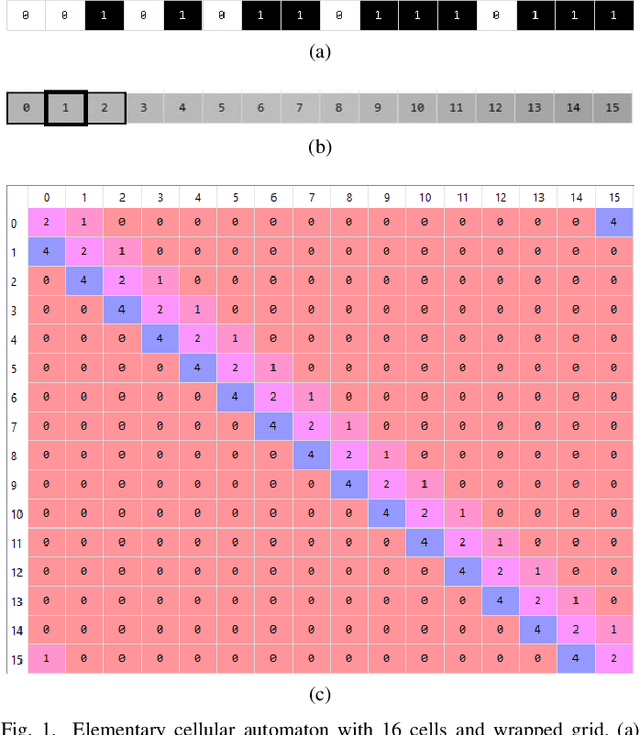
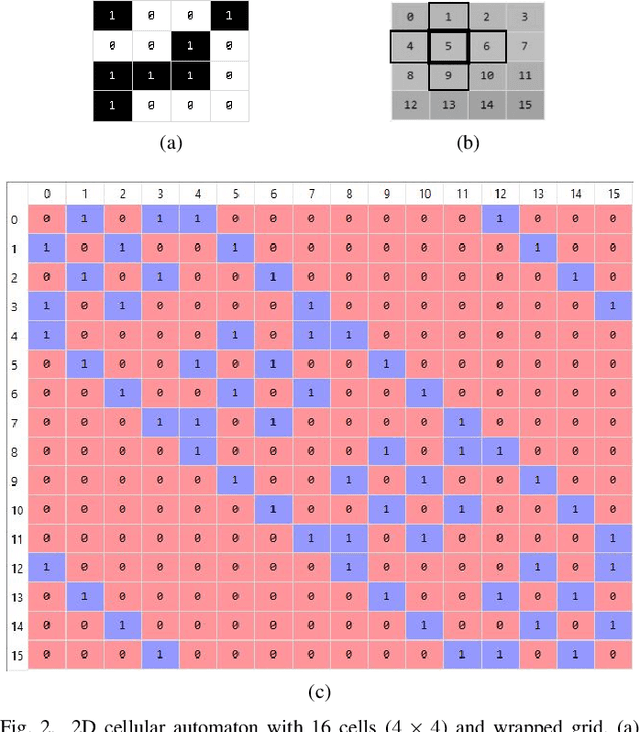
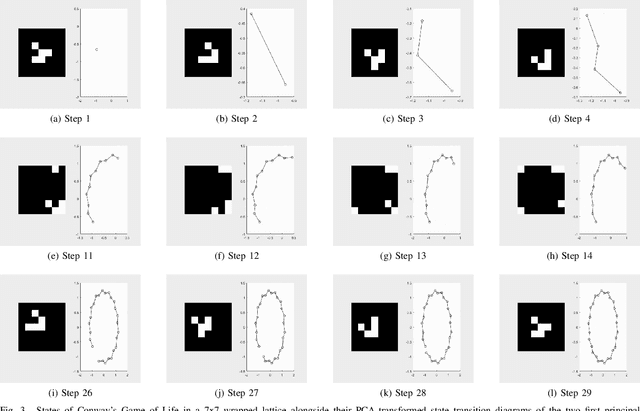
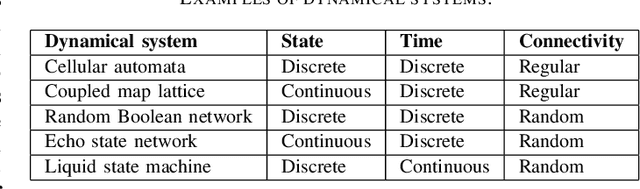
Dynamical systems are capable of performing computation in a reservoir computing paradigm. This paper presents a general representation of these systems as an artificial neural network (ANN). Initially, we implement the simplest dynamical system, a cellular automaton. The mathematical fundamentals behind an ANN are maintained, but the weights of the connections and the activation function are adjusted to work as an update rule in the context of cellular automata. The advantages of such implementation are its usage on specialized and optimized deep learning libraries, the capabilities to generalize it to other types of networks and the possibility to evolve cellular automata and other dynamical systems in terms of connectivity, update and learning rules. Our implementation of cellular automata constitutes an initial step towards a general framework for dynamical systems. It aims to evolve such systems to optimize their usage in reservoir computing and to model physical computing substrates.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge