Query-decision Regression between Shortest Path and Minimum Steiner Tree

Considering a graph with unknown weights, can we find the shortest path for a pair of nodes if we know the minimal Steiner trees associated with some subset of nodes? That is, with respect to a fixed latent decision-making system (e.g., a weighted graph), we seek to solve one optimization problem (e.g., the shortest path problem) by leveraging information associated with another optimization problem (e.g., the minimal Steiner tree problem). In this paper, we study such a prototype problem called \textit{query-decision regression with task shifts}, focusing on the shortest path problem and the minimum Steiner tree problem. We provide theoretical insights regarding the design of realizable hypothesis spaces for building scoring models, and present two principled learning frameworks. Our experimental studies show that such problems can be solved to a decent extent with statistical significance.

VN-Solver: Vision-based Neural Solver for Combinatorial Optimization over Graphs

Data-driven approaches have been proven effective in solving combinatorial optimization problems over graphs such as the traveling salesman problems and the vehicle routing problem. The rationale behind such methods is that the input instances may follow distributions with salient patterns that can be leveraged to overcome the worst-case computational hardness. For optimization problems over graphs, the common practice of neural combinatorial solvers consumes the inputs in the form of adjacency matrices. In this paper, we explore a vision-based method that is conceptually novel: can neural models solve graph optimization problems by \textit{taking a look at the graph pattern}? Our results suggest that the performance of such vision-based methods is not only non-trivial but also comparable to the state-of-the-art matrix-based methods, which opens a new avenue for developing data-driven optimization solvers.

Social-Inverse: Inverse Decision-making of Social Contagion Management with Task Migrations

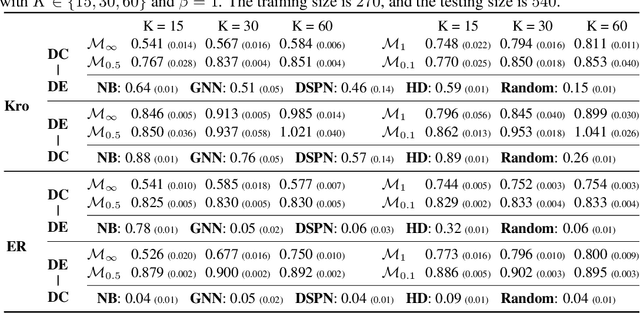
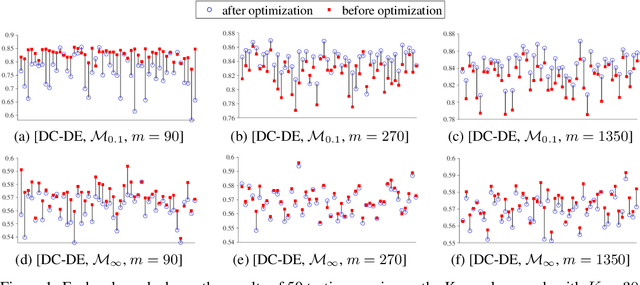
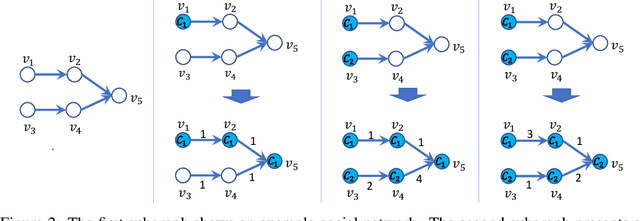
Considering two decision-making tasks $A$ and $B$, each of which wishes to compute an effective \textit{decision} $Y$ for a given \textit{query} $X$, {can we solve task $B$ by using query-decision pairs $(X, Y)$ of $A$ without knowing the latent decision-making model?} Such problems, called \textit{inverse decision-making with task migrations}, are of interest in that the complex and stochastic nature of real-world applications often prevents the agent from completely knowing the underlying system. In this paper, we introduce such a new problem with formal formulations and present a generic framework for addressing decision-making tasks in social contagion management. On the theory side, we present a generalization analysis for justifying the learning performance of our framework. In empirical studies, we perform a sanity check and compare the presented method with other possible learning-based and graph-based methods. We have acquired promising experimental results, confirming for the first time that it is possible to solve one decision-making task by using the solutions associated with another one.

Learning the Propagation of Worms in Wireless Sensor Networks

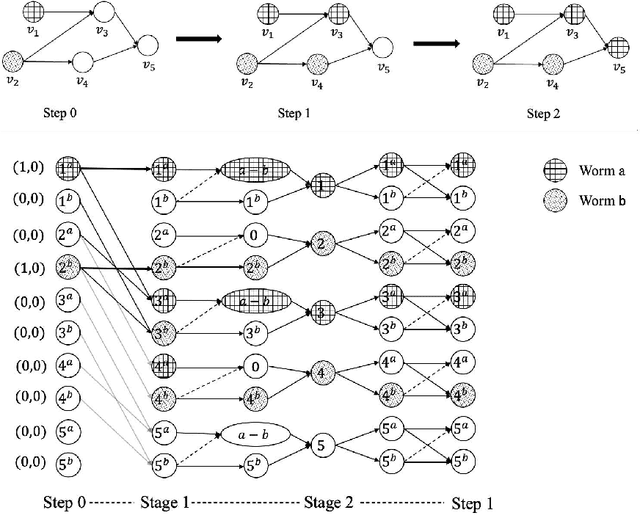
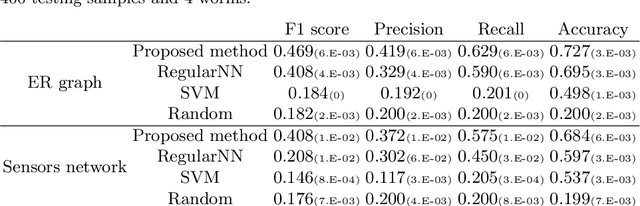
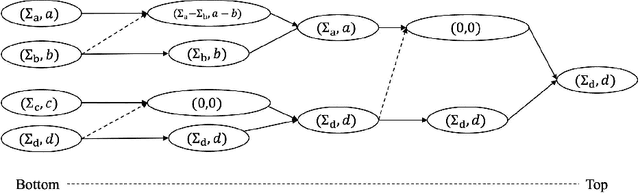
Wireless sensor networks (WSNs) are composed of spatially distributed sensors and are considered vulnerable to attacks by worms and their variants. Due to the distinct strategies of worms propagation, the dynamic behavior varies depending on the different features of the sensors. Modeling the spread of worms can help us understand the worm attack behaviors and analyze the propagation procedure. In this paper, we design a communication model under various worms. We aim to learn our proposed model to analytically derive the dynamics of competitive worms propagation. We develop a new searching space combined with complex neural network models. Furthermore, the experiment results verified our analysis and demonstrated the performance of our proposed learning algorithms.

Deep-Steiner: Learning to Solve the Euclidean Steiner Tree Problem

The Euclidean Steiner tree problem seeks the min-cost network to connect a collection of target locations, and it underlies many applications of wireless networks. In this paper, we present a study on solving the Euclidean Steiner tree problem using reinforcement learning enhanced by graph representation learning. Different from the commonly studied connectivity problems like travelling salesman problem or vehicle routing problem where the search space is finite, the Euclidean Steiner tree problem requires to search over the entire Euclidean space, thereby making the existing methods not applicable. In this paper, we design discretization methods by leveraging the unique characteristics of the Steiner tree, and propose new training schemes for handling the dynamic Steiner points emerging during the incremental construction. Our design is examined through a sanity check using experiments on a collection of datasets, with encouraging results demonstrating the utility of our method as an alternative to classic combinatorial methods.

Learnability of Competitive Threshold Models

Modeling the spread of social contagions is central to various applications in social computing. In this paper, we study the learnability of the competitive threshold model from a theoretical perspective. We demonstrate how competitive threshold models can be seamlessly simulated by artificial neural networks with finite VC dimensions, which enables analytical sample complexity and generalization bounds. Based on the proposed hypothesis space, we design efficient algorithms under the empirical risk minimization scheme. The theoretical insights are finally translated into practical and explainable modeling methods, the effectiveness of which is verified through a sanity check over a few synthetic and real datasets. The experimental results promisingly show that our method enjoys a decent performance without using excessive data points, outperforming off-the-shelf methods.

USCO-Solver: Solving Undetermined Stochastic Combinatorial Optimization Problems

Real-world decision-making systems are often subject to uncertainties that have to be resolved through observational data. Therefore, we are frequently confronted with combinatorial optimization problems of which the objective function is unknown and thus has to be debunked using empirical evidence. In contrast to the common practice that relies on a learning-and-optimization strategy, we consider the regression between combinatorial spaces, aiming to infer high-quality optimization solutions from samples of input-solution pairs -- without the need to learn the objective function. Our main deliverable is a universal solver that is able to handle abstract undetermined stochastic combinatorial optimization problems. For learning foundations, we present learning-error analysis under the PAC-Bayesian framework using a new margin-based analysis. In empirical studies, we demonstrate our design using proof-of-concept experiments, and compare it with other methods that are potentially applicable. Overall, we obtain highly encouraging experimental results for several classic combinatorial problems on both synthetic and real-world datasets.

StratLearner: Learning a Strategy for Misinformation Prevention in Social Networks

Given a combinatorial optimization problem taking an input, can we learn a strategy to solve it from the examples of input-solution pairs without knowing its objective function? In this paper, we consider such a setting and study the misinformation prevention problem. Given the examples of attacker-protector pairs, our goal is to learn a strategy to compute protectors against future attackers, without the need of knowing the underlying diffusion model. To this end, we design a structured prediction framework, where the main idea is to parameterize the scoring function using random features constructed through distance functions on randomly sampled subgraphs, which leads to a kernelized scoring function with weights learnable via the large margin method. Evidenced by experiments, our method can produce near-optimal protectors without using any information of the diffusion model, and it outperforms other possible graph-based and learning-based methods by an evident margin.