Guangliang Chen
High Dimensional Data Modeling Techniques for Detection of Chemical Plumes and Anomalies in Hyperspectral Images and Movies
Jan 29, 2016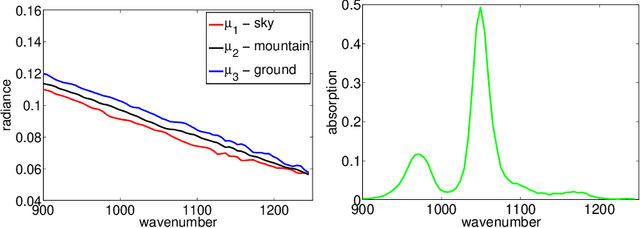
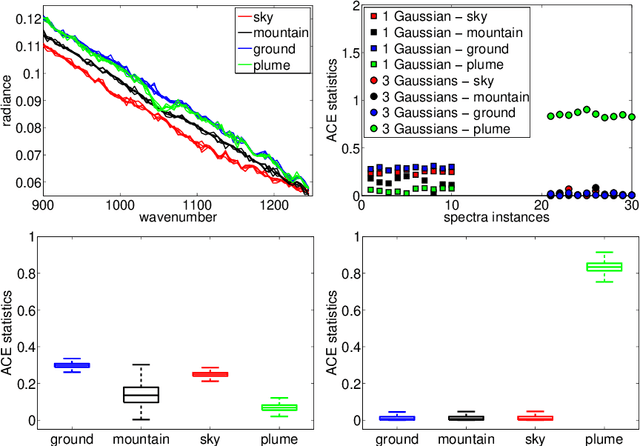
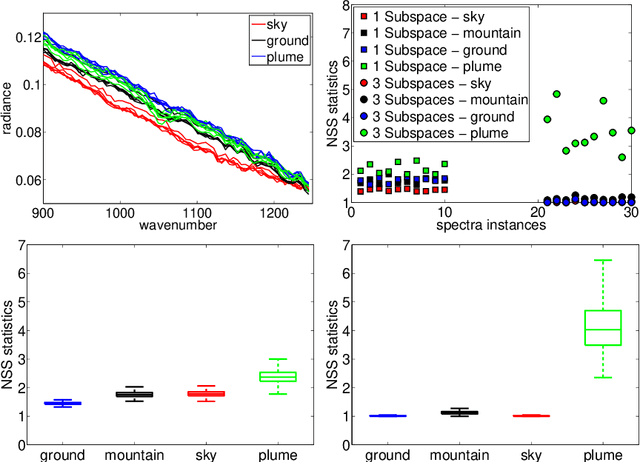
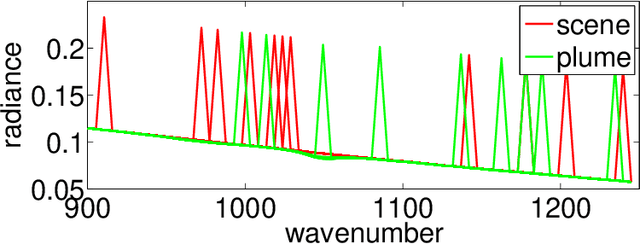
Abstract:We briefly review recent progress in techniques for modeling and analyzing hyperspectral images and movies, in particular for detecting plumes of both known and unknown chemicals. For detecting chemicals of known spectrum, we extend the technique of using a single subspace for modeling the background to a "mixture of subspaces" model to tackle more complicated background. Furthermore, we use partial least squares regression on a resampled training set to boost performance. For the detection of unknown chemicals we view the problem as an anomaly detection problem, and use novel estimators with low-sampled complexity for intrinsically low-dimensional data in high-dimensions that enable us to model the "normal" spectra and detect anomalies. We apply these algorithms to benchmark data sets made available by the Automated Target Detection program co-funded by NSF, DTRA and NGA, and compare, when applicable, to current state-of-the-art algorithms, with favorable results.
Spectral clustering based on local linear approximations
Nov 29, 2011



Abstract:In the context of clustering, we assume a generative model where each cluster is the result of sampling points in the neighborhood of an embedded smooth surface; the sample may be contaminated with outliers, which are modeled as points sampled in space away from the clusters. We consider a prototype for a higher-order spectral clustering method based on the residual from a local linear approximation. We obtain theoretical guarantees for this algorithm and show that, in terms of both separation and robustness to outliers, it outperforms the standard spectral clustering algorithm (based on pairwise distances) of Ng, Jordan and Weiss (NIPS '01). The optimal choice for some of the tuning parameters depends on the dimension and thickness of the clusters. We provide estimators that come close enough for our theoretical purposes. We also discuss the cases of clusters of mixed dimensions and of clusters that are generated from smoother surfaces. In our experiments, this algorithm is shown to outperform pairwise spectral clustering on both simulated and real data.
Multiscale Geometric Methods for Data Sets II: Geometric Multi-Resolution Analysis
Sep 08, 2011



Abstract:Data sets are often modeled as point clouds in $R^D$, for $D$ large. It is often assumed that the data has some interesting low-dimensional structure, for example that of a $d$-dimensional manifold $M$, with $d$ much smaller than $D$. When $M$ is simply a linear subspace, one may exploit this assumption for encoding efficiently the data by projecting onto a dictionary of $d$ vectors in $R^D$ (for example found by SVD), at a cost $(n+D)d$ for $n$ data points. When $M$ is nonlinear, there are no "explicit" constructions of dictionaries that achieve a similar efficiency: typically one uses either random dictionaries, or dictionaries obtained by black-box optimization. In this paper we construct data-dependent multi-scale dictionaries that aim at efficient encoding and manipulating of the data. Their construction is fast, and so are the algorithms that map data points to dictionary coefficients and vice versa. In addition, data points are guaranteed to have a sparse representation in terms of the dictionary. We think of dictionaries as the analogue of wavelets, but for approximating point clouds rather than functions.
Foundations of a Multi-way Spectral Clustering Framework for Hybrid Linear Modeling
Jan 15, 2009


Abstract:The problem of Hybrid Linear Modeling (HLM) is to model and segment data using a mixture of affine subspaces. Different strategies have been proposed to solve this problem, however, rigorous analysis justifying their performance is missing. This paper suggests the Theoretical Spectral Curvature Clustering (TSCC) algorithm for solving the HLM problem, and provides careful analysis to justify it. The TSCC algorithm is practically a combination of Govindu's multi-way spectral clustering framework (CVPR 2005) and Ng et al.'s spectral clustering algorithm (NIPS 2001). The main result of this paper states that if the given data is sampled from a mixture of distributions concentrated around affine subspaces, then with high sampling probability the TSCC algorithm segments well the different underlying clusters. The goodness of clustering depends on the within-cluster errors, the between-clusters interaction, and a tuning parameter applied by TSCC. The proof also provides new insights for the analysis of Ng et al. (NIPS 2001).
* 40 pages. Minor changes to the previous version (mainly revised Sections 2.2 & 2.3, and added references). Accepted to the Journal of Foundations of Computational Mathematics
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge