Accelerating Inference of Networks in the Frequency Domain

It has been demonstrated that networks' parameters can be significantly reduced in the frequency domain with a very small decrease in accuracy. However, given the cost of frequency transforms, the computational complexity is not significantly decreased. In this work, we propose performing network inference in the frequency domain to speed up networks whose frequency parameters are sparse. In particular, we propose a frequency inference chain that is dual to the network inference in the spatial domain. In order to handle the non-linear layers, we make a compromise to apply non-linear operations on frequency data directly, which works effectively. Enabled by the frequency inference chain and the strategy for non-linear layers, the proposed approach completes the entire inference in the frequency domain. Unlike previous approaches which require extra frequency or inverse transforms for all layers, the proposed approach only needs the frequency transform and its inverse once at the beginning and once at the end of a network. Comparisons with state-of-the-art methods demonstrate that the proposed approach significantly improves accuracy in the case of a high speedup ratio (over 100x). The source code is available at \url{https://github.com/guanfangdong/FreqNet-Infer}.

Deep Clustering via Distribution Learning

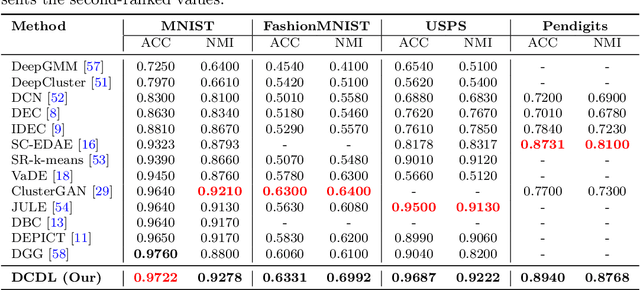
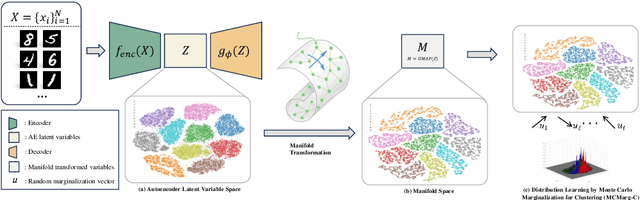
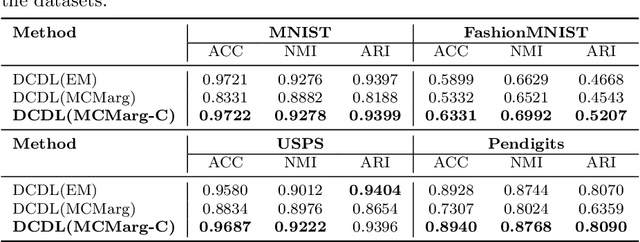
Distribution learning finds probability density functions from a set of data samples, whereas clustering aims to group similar data points to form clusters. Although there are deep clustering methods that employ distribution learning methods, past work still lacks theoretical analysis regarding the relationship between clustering and distribution learning. Thus, in this work, we provide a theoretical analysis to guide the optimization of clustering via distribution learning. To achieve better results, we embed deep clustering guided by a theoretical analysis. Furthermore, the distribution learning method cannot always be directly applied to data. To overcome this issue, we introduce a clustering-oriented distribution learning method called Monte-Carlo Marginalization for Clustering. We integrate Monte-Carlo Marginalization for Clustering into Deep Clustering, resulting in Deep Clustering via Distribution Learning (DCDL). Eventually, the proposed DCDL achieves promising results compared to state-of-the-art methods on popular datasets. Considering a clustering task, the new distribution learning method outperforms previous methods as well.

Medical Image Denosing via Explainable AI Feature Preserving Loss

Denoising algorithms play a crucial role in medical image processing and analysis. However, classical denoising algorithms often ignore explanatory and critical medical features preservation, which may lead to misdiagnosis and legal liabilities. In this work, we propose a new denoising method for medical images that not only efficiently removes various types of noise, but also preserves key medical features throughout the process. To achieve this goal, we utilize a gradient-based eXplainable Artificial Intelligence (XAI) approach to design a feature preserving loss function. Our feature preserving loss function is motivated by the characteristic that gradient-based XAI is sensitive to noise. Through backpropagation, medical image features before and after denoising can be kept consistent. We conducted extensive experiments on three available medical image datasets, including synthesized 13 different types of noise and artifacts. The experimental results demonstrate the superiority of our method in terms of denoising performance, model explainability, and generalization.

Affine-Transformation-Invariant Image Classification by Differentiable Arithmetic Distribution Module

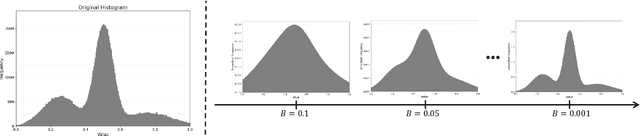
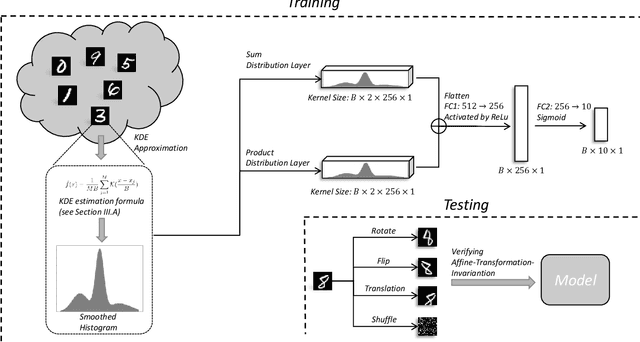
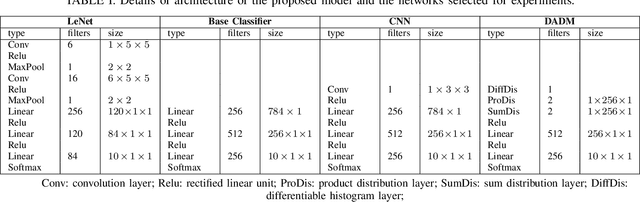
Although Convolutional Neural Networks (CNNs) have achieved promising results in image classification, they still are vulnerable to affine transformations including rotation, translation, flip and shuffle. The drawback motivates us to design a module which can alleviate the impact from different affine transformations. Thus, in this work, we introduce a more robust substitute by incorporating distribution learning techniques, focusing particularly on learning the spatial distribution information of pixels in images. To rectify the issue of non-differentiability of prior distribution learning methods that rely on traditional histograms, we adopt the Kernel Density Estimation (KDE) to formulate differentiable histograms. On this foundation, we present a novel Differentiable Arithmetic Distribution Module (DADM), which is designed to extract the intrinsic probability distributions from images. The proposed approach is able to enhance the model's robustness to affine transformations without sacrificing its feature extraction capabilities, thus bridging the gap between traditional CNNs and distribution-based learning. We validate the effectiveness of the proposed approach through ablation study and comparative experiments with LeNet.

Bridging Distribution Learning and Image Clustering in High-dimensional Space

Distribution learning focuses on learning the probability density function from a set of data samples. In contrast, clustering aims to group similar objects together in an unsupervised manner. Usually, these two tasks are considered unrelated. However, the relationship between the two may be indirectly correlated, with Gaussian Mixture Models (GMM) acting as a bridge. In this paper, we focus on exploring the correlation between distribution learning and clustering, with the motivation to fill the gap between these two fields, utilizing an autoencoder (AE) to encode images into a high-dimensional latent space. Then, Monte-Carlo Marginalization (MCMarg) and Kullback-Leibler (KL) divergence loss are used to fit the Gaussian components of the GMM and learn the data distribution. Finally, image clustering is achieved through each Gaussian component of GMM. Yet, the "curse of dimensionality" poses severe challenges for most clustering algorithms. Compared with the classic Expectation-Maximization (EM) Algorithm, experimental results show that MCMarg and KL divergence can greatly alleviate the difficulty. Based on the experimental results, we believe distribution learning can exploit the potential of GMM in image clustering within high-dimensional space.

Is Deep Learning Network Necessary for Image Generation?

Recently, images are considered samples from a high-dimensional distribution, and deep learning has become almost synonymous with image generation. However, is a deep learning network truly necessary for image generation? In this paper, we investigate the possibility of image generation without using a deep learning network, motivated by validating the assumption that images follow a high-dimensional distribution. Since images are assumed to be samples from such a distribution, we utilize the Gaussian Mixture Model (GMM) to describe it. In particular, we employ a recent distribution learning technique named as Monte-Carlo Marginalization to capture the parameters of the GMM based on image samples. Moreover, we also use the Singular Value Decomposition (SVD) for dimensionality reduction to decrease computational complexity. During our evaluation experiment, we first attempt to model the distribution of image samples directly to verify the assumption that images truly follow a distribution. We then use the SVD for dimensionality reduction. The principal components, rather than raw image data, are used for distribution learning. Compared to methods relying on deep learning networks, our approach is more explainable, and its performance is promising. Experiments show that our images have a lower FID value compared to those generated by variational auto-encoders, demonstrating the feasibility of image generation without deep learning networks.

Learning Distributions via Monte-Carlo Marginalization

We propose a novel method to learn intractable distributions from their samples. The main idea is to use a parametric distribution model, such as a Gaussian Mixture Model (GMM), to approximate intractable distributions by minimizing the KL-divergence. Based on this idea, there are two challenges that need to be addressed. First, the computational complexity of KL-divergence is unacceptable when the dimensions of distributions increases. The Monte-Carlo Marginalization (MCMarg) is proposed to address this issue. The second challenge is the differentiability of the optimization process, since the target distribution is intractable. We handle this problem by using Kernel Density Estimation (KDE). The proposed approach is a powerful tool to learn complex distributions and the entire process is differentiable. Thus, it can be a better substitute of the variational inference in variational auto-encoders (VAE). One strong evidence of the benefit of our method is that the distributions learned by the proposed approach can generate better images even based on a pre-trained VAE's decoder. Based on this point, we devise a distribution learning auto-encoder which is better than VAE under the same network architecture. Experiments on standard dataset and synthetic data demonstrate the efficiency of the proposed approach.

Frequency Regularization: Restricting Information Redundancy of Convolutional Neural Networks

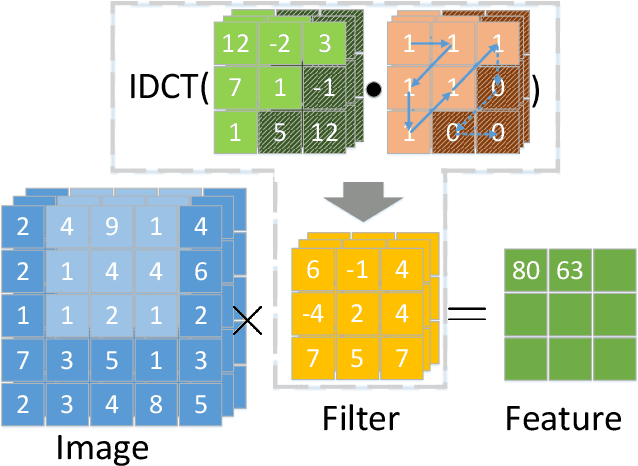
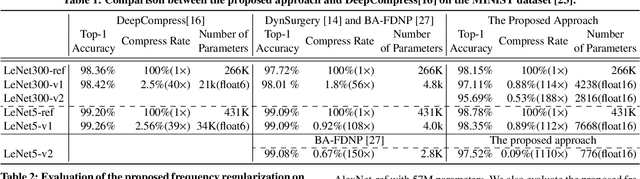
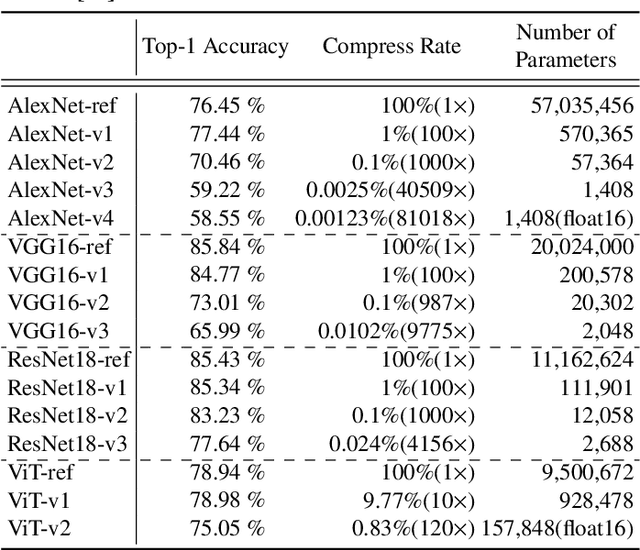
Convolutional neural networks have demonstrated impressive results in many computer vision tasks. However, the increasing size of these networks raises concerns about the information overload resulting from the large number of network parameters. In this paper, we propose Frequency Regularization to restrict the non-zero elements of the network parameters in the frequency domain. The proposed approach operates at the tensor level, and can be applied to almost all network architectures. Specifically, the tensors of parameters are maintained in the frequency domain, where high frequency components can be eliminated by zigzag setting tensor elements to zero. Then, the inverse discrete cosine transform (IDCT) is used to reconstruct the spatial tensors for matrix operations during network training. Since high frequency components of images are known to be less critical, a large proportion of these parameters can be set to zero when networks are trained with the proposed frequency regularization. Comprehensive evaluations on various state-of-the-art network architectures, including LeNet, Alexnet, VGG, Resnet, ViT, UNet, GAN, and VAE, demonstrate the effectiveness of the proposed frequency regularization. For a very small accuracy decrease (less than 2\%), a LeNet5 with 0.4M parameters can be represented by only 776 float16 numbers (over 1100$\times$ reduction), and a UNet with 34M parameters can be represented by only 759 float16 numbers (over 80000$\times$ reduction). In particular, the original size of the UNet model is 366MB, we reduce it to 4.5kb.

Learning Temporal Distribution and Spatial Correlation for Universal Moving Object Segmentation

Universal moving object segmentation aims to provide a general model for videos from all types of natural scenes, as previous approaches are usually effective for specific or similar scenes. In this paper, we propose a method called Learning Temporal Distribution and Spatial Correlation (LTS) that has the potential to be a general solution for universal moving object segmentation. In the proposed approach, the distribution from temporal pixels is first learned by our Defect Iterative Distribution Learning (DIDL) network for a scene-independent segmentation. Then, the Stochastic Bayesian Refinement (SBR) Network, which learns the spatial correlation, is proposed to improve the binary mask generated by the DIDL network. Benefiting from the scene independence of the temporal distribution and the accuracy improvement resulting from the spatial correlation, the proposed approach performs well for almost all videos from diverse and complex natural scenes with fixed parameters. Comprehensive experiments on standard datasets including LASIESTA, CDNet2014, BMC, SBMI2015 and 128 real world videos demonstrate the superiority of proposed approach compared to state-of-the-art methods with or without the use of deep learning networks. To the best of our knowledge, this work has high potential to be a general solution for moving object segmentation in real world environments.

SPGNet: Spatial Projection Guided 3D Human Pose Estimation in Low Dimensional Space

We propose a method SPGNet for 3D human pose estimation that mixes multi-dimensional re-projection into supervised learning. In this method, the 2D-to-3D-lifting network predicts the global position and coordinates of the 3D human pose. Then, we re-project the estimated 3D pose back to the 2D key points along with spatial adjustments. The loss functions compare the estimated 3D pose with the 3D pose ground truth, and re-projected 2D pose with the input 2D pose. In addition, we propose a kinematic constraint to restrict the predicted target with constant human bone length. Based on the estimation results for the dataset Human3.6M, our approach outperforms many state-of-the-art methods both qualitatively and quantitatively.