Frequency Regularization: Restricting Information Redundancy of Convolutional Neural Networks
Paper and Code
Apr 30, 2023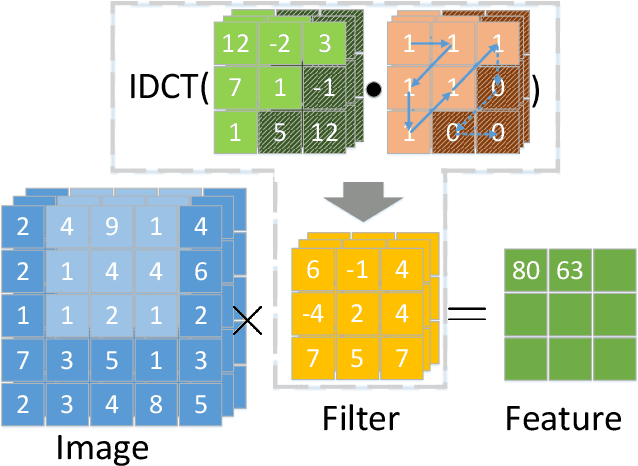
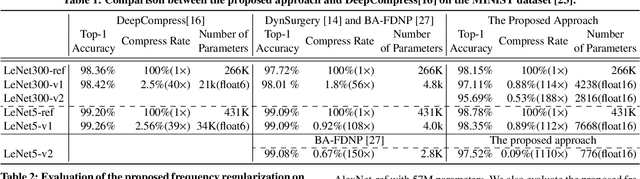
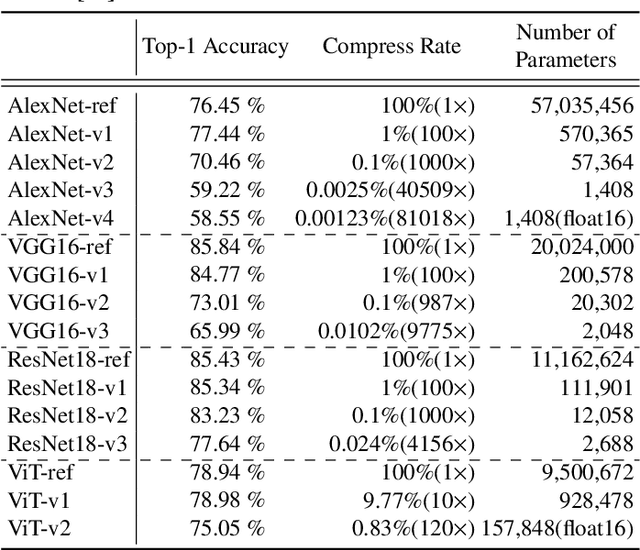

Convolutional neural networks have demonstrated impressive results in many computer vision tasks. However, the increasing size of these networks raises concerns about the information overload resulting from the large number of network parameters. In this paper, we propose Frequency Regularization to restrict the non-zero elements of the network parameters in the frequency domain. The proposed approach operates at the tensor level, and can be applied to almost all network architectures. Specifically, the tensors of parameters are maintained in the frequency domain, where high frequency components can be eliminated by zigzag setting tensor elements to zero. Then, the inverse discrete cosine transform (IDCT) is used to reconstruct the spatial tensors for matrix operations during network training. Since high frequency components of images are known to be less critical, a large proportion of these parameters can be set to zero when networks are trained with the proposed frequency regularization. Comprehensive evaluations on various state-of-the-art network architectures, including LeNet, Alexnet, VGG, Resnet, ViT, UNet, GAN, and VAE, demonstrate the effectiveness of the proposed frequency regularization. For a very small accuracy decrease (less than 2\%), a LeNet5 with 0.4M parameters can be represented by only 776 float16 numbers (over 1100$\times$ reduction), and a UNet with 34M parameters can be represented by only 759 float16 numbers (over 80000$\times$ reduction). In particular, the original size of the UNet model is 366MB, we reduce it to 4.5kb.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge