Deep Clustering via Distribution Learning

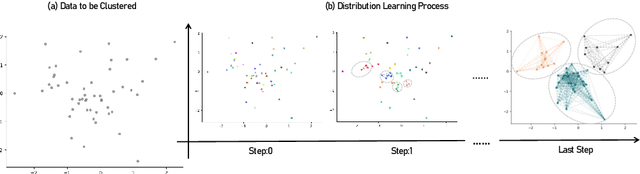
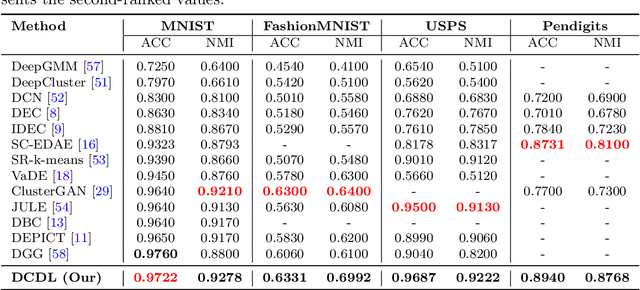
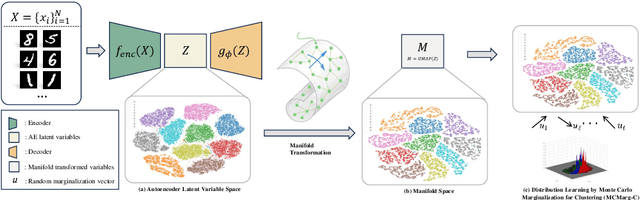
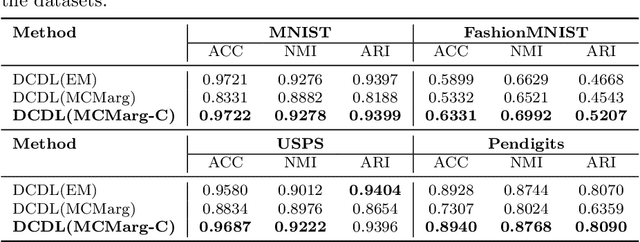
Distribution learning finds probability density functions from a set of data samples, whereas clustering aims to group similar data points to form clusters. Although there are deep clustering methods that employ distribution learning methods, past work still lacks theoretical analysis regarding the relationship between clustering and distribution learning. Thus, in this work, we provide a theoretical analysis to guide the optimization of clustering via distribution learning. To achieve better results, we embed deep clustering guided by a theoretical analysis. Furthermore, the distribution learning method cannot always be directly applied to data. To overcome this issue, we introduce a clustering-oriented distribution learning method called Monte-Carlo Marginalization for Clustering. We integrate Monte-Carlo Marginalization for Clustering into Deep Clustering, resulting in Deep Clustering via Distribution Learning (DCDL). Eventually, the proposed DCDL achieves promising results compared to state-of-the-art methods on popular datasets. Considering a clustering task, the new distribution learning method outperforms previous methods as well.

Affine-Transformation-Invariant Image Classification by Differentiable Arithmetic Distribution Module

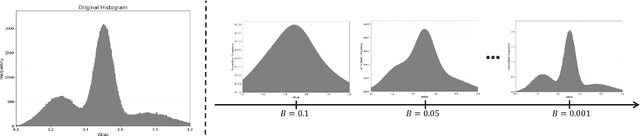
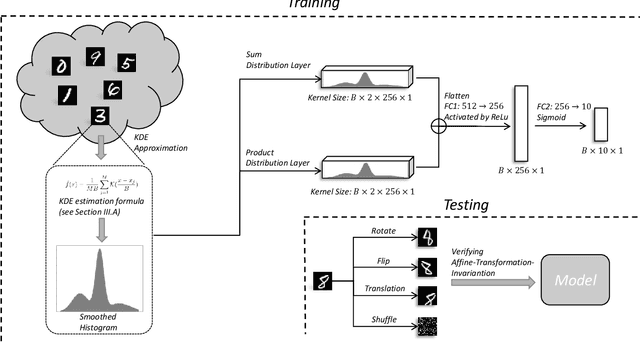
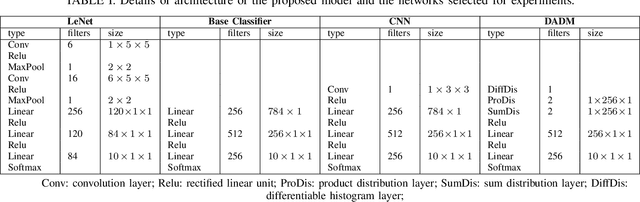
Although Convolutional Neural Networks (CNNs) have achieved promising results in image classification, they still are vulnerable to affine transformations including rotation, translation, flip and shuffle. The drawback motivates us to design a module which can alleviate the impact from different affine transformations. Thus, in this work, we introduce a more robust substitute by incorporating distribution learning techniques, focusing particularly on learning the spatial distribution information of pixels in images. To rectify the issue of non-differentiability of prior distribution learning methods that rely on traditional histograms, we adopt the Kernel Density Estimation (KDE) to formulate differentiable histograms. On this foundation, we present a novel Differentiable Arithmetic Distribution Module (DADM), which is designed to extract the intrinsic probability distributions from images. The proposed approach is able to enhance the model's robustness to affine transformations without sacrificing its feature extraction capabilities, thus bridging the gap between traditional CNNs and distribution-based learning. We validate the effectiveness of the proposed approach through ablation study and comparative experiments with LeNet.

Frequency Regularization: Restricting Information Redundancy of Convolutional Neural Networks

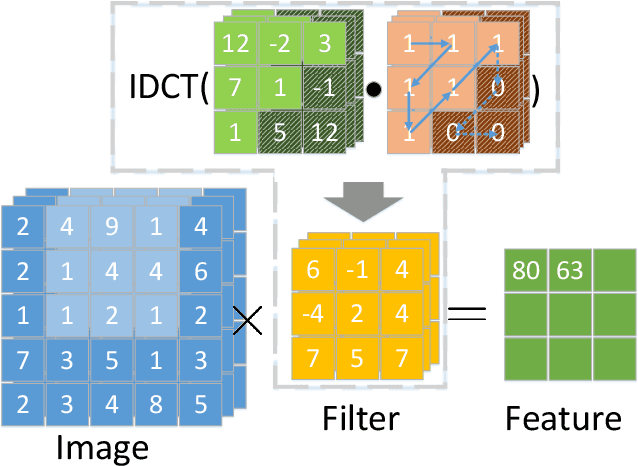
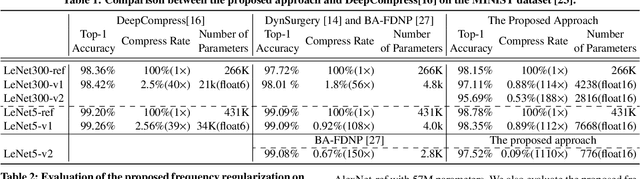
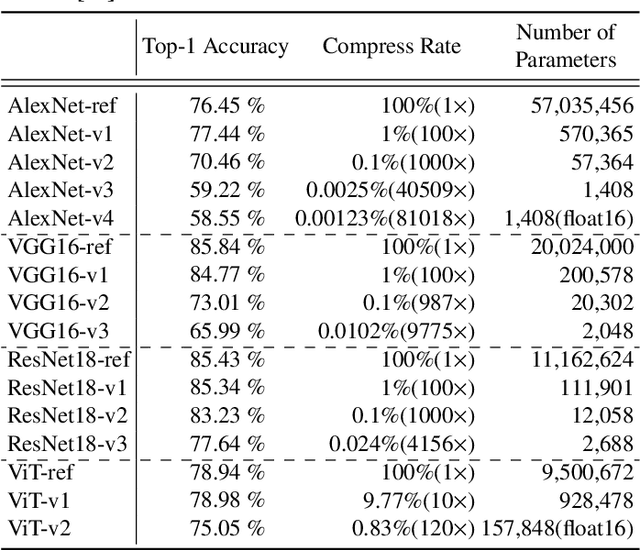
Convolutional neural networks have demonstrated impressive results in many computer vision tasks. However, the increasing size of these networks raises concerns about the information overload resulting from the large number of network parameters. In this paper, we propose Frequency Regularization to restrict the non-zero elements of the network parameters in the frequency domain. The proposed approach operates at the tensor level, and can be applied to almost all network architectures. Specifically, the tensors of parameters are maintained in the frequency domain, where high frequency components can be eliminated by zigzag setting tensor elements to zero. Then, the inverse discrete cosine transform (IDCT) is used to reconstruct the spatial tensors for matrix operations during network training. Since high frequency components of images are known to be less critical, a large proportion of these parameters can be set to zero when networks are trained with the proposed frequency regularization. Comprehensive evaluations on various state-of-the-art network architectures, including LeNet, Alexnet, VGG, Resnet, ViT, UNet, GAN, and VAE, demonstrate the effectiveness of the proposed frequency regularization. For a very small accuracy decrease (less than 2\%), a LeNet5 with 0.4M parameters can be represented by only 776 float16 numbers (over 1100$\times$ reduction), and a UNet with 34M parameters can be represented by only 759 float16 numbers (over 80000$\times$ reduction). In particular, the original size of the UNet model is 366MB, we reduce it to 4.5kb.