On Robot Grasp Learning Using Equivariant Models

Real-world grasp detection is challenging due to the stochasticity in grasp dynamics and the noise in hardware. Ideally, the system would adapt to the real world by training directly on physical systems. However, this is generally difficult due to the large amount of training data required by most grasp learning models. In this paper, we note that the planar grasp function is $\SE(2)$-equivariant and demonstrate that this structure can be used to constrain the neural network used during learning. This creates an inductive bias that can significantly improve the sample efficiency of grasp learning and enable end-to-end training from scratch on a physical robot with as few as $600$ grasp attempts. We call this method Symmetric Grasp learning (SymGrasp) and show that it can learn to grasp ``from scratch'' in less that 1.5 hours of physical robot time.

SEIL: Simulation-augmented Equivariant Imitation Learning

In robotic manipulation, acquiring samples is extremely expensive because it often requires interacting with the real world. Traditional image-level data augmentation has shown the potential to improve sample efficiency in various machine learning tasks. However, image-level data augmentation is insufficient for an imitation learning agent to learn good manipulation policies in a reasonable amount of demonstrations. We propose Simulation-augmented Equivariant Imitation Learning (SEIL), a method that combines a novel data augmentation strategy of supplementing expert trajectories with simulated transitions and an equivariant model that exploits the $\mathrm{O}(2)$ symmetry in robotic manipulation. Experimental evaluations demonstrate that our method can learn non-trivial manipulation tasks within ten demonstrations and outperforms the baselines with a significant margin.

Sample Efficient Grasp Learning Using Equivariant Models

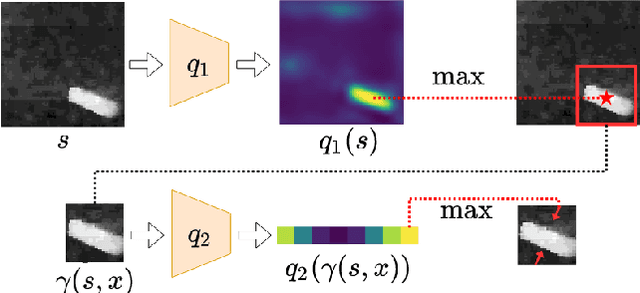
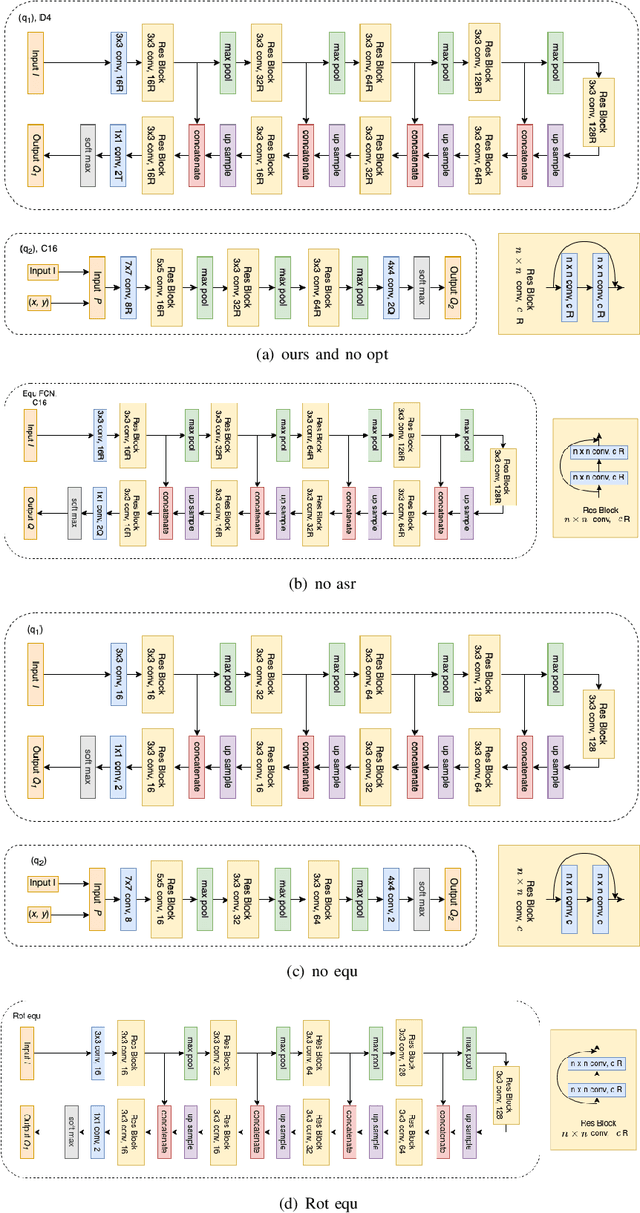
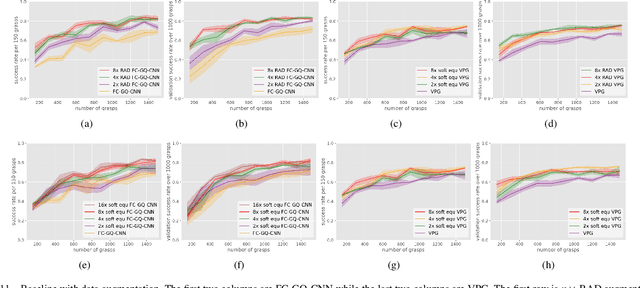
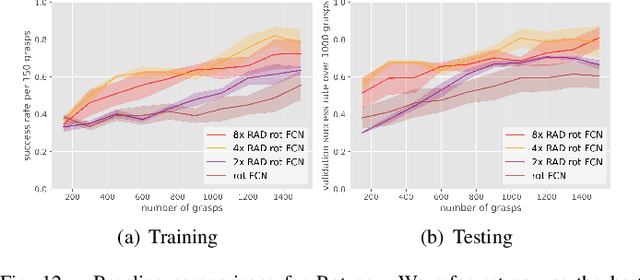
In planar grasp detection, the goal is to learn a function from an image of a scene onto a set of feasible grasp poses in $\mathrm{SE}(2)$. In this paper, we recognize that the optimal grasp function is $\mathrm{SE}(2)$-equivariant and can be modeled using an equivariant convolutional neural network. As a result, we are able to significantly improve the sample efficiency of grasp learning, obtaining a good approximation of the grasp function after only 600 grasp attempts. This is few enough that we can learn to grasp completely on a physical robot in about 1.5 hours.