Image Denoising: The Deep Learning Revolution and Beyond -- A Survey Paper --

Image denoising (removal of additive white Gaussian noise from an image) is one of the oldest and most studied problems in image processing. An extensive work over several decades has led to thousands of papers on this subject, and to many well-performing algorithms for this task. Indeed, 10 years ago, these achievements have led some researchers to suspect that "Denoising is Dead", in the sense that all that can be achieved in this domain has already been obtained. However, this turned out to be far from the truth, with the penetration of deep learning (DL) into image processing. The era of DL brought a revolution to image denoising, both by taking the lead in today's ability for noise removal in images, and by broadening the scope of denoising problems being treated. Our paper starts by describing this evolution, highlighting in particular the tension and synergy that exist between classical approaches and modern DL-based alternatives in design of image denoisers. The recent transitions in the field of image denoising go far beyond the ability to design better denoisers. In the 2nd part of this paper we focus on recently discovered abilities and prospects of image denoisers. We expose the possibility of using denoisers to serve other problems, such as regularizing general inverse problems and serving as the prime engine in diffusion-based image synthesis. We also unveil the idea that denoising and other inverse problems might not have a unique solution as common algorithms would have us believe. Instead, we describe constructive ways to produce randomized and diverse high quality results for inverse problems, all fueled by the progress that DL brought to image denoising. This survey paper aims to provide a broad view of the history of image denoising and closely related topics. Our aim is to give a better context to recent discoveries, and to the influence of DL in our domain.

Patch-Craft Self-Supervised Training for Correlated Image Denoising

Supervised neural networks are known to achieve excellent results in various image restoration tasks. However, such training requires datasets composed of pairs of corrupted images and their corresponding ground truth targets. Unfortunately, such data is not available in many applications. For the task of image denoising in which the noise statistics is unknown, several self-supervised training methods have been proposed for overcoming this difficulty. Some of these require knowledge of the noise model, while others assume that the contaminating noise is uncorrelated, both assumptions are too limiting for many practical needs. This work proposes a novel self-supervised training technique suitable for the removal of unknown correlated noise. The proposed approach neither requires knowledge of the noise model nor access to ground truth targets. The input to our algorithm consists of easily captured bursts of noisy shots. Our algorithm constructs artificial patch-craft images from these bursts by patch matching and stitching, and the obtained crafted images are used as targets for the training. Our method does not require registration of the images within the burst. We evaluate the proposed framework through extensive experiments with synthetic and real image noise.

SNIPS: Solving Noisy Inverse Problems Stochastically

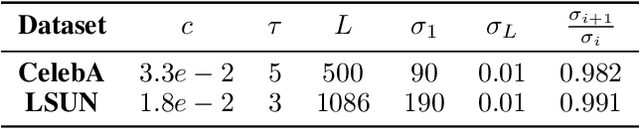
In this work we introduce a novel stochastic algorithm dubbed SNIPS, which draws samples from the posterior distribution of any linear inverse problem, where the observation is assumed to be contaminated by additive white Gaussian noise. Our solution incorporates ideas from Langevin dynamics and Newton's method, and exploits a pre-trained minimum mean squared error (MMSE) Gaussian denoiser. The proposed approach relies on an intricate derivation of the posterior score function that includes a singular value decomposition (SVD) of the degradation operator, in order to obtain a tractable iterative algorithm for the desired sampling. Due to its stochasticity, the algorithm can produce multiple high perceptual quality samples for the same noisy observation. We demonstrate the abilities of the proposed paradigm for image deblurring, super-resolution, and compressive sensing. We show that the samples produced are sharp, detailed and consistent with the given measurements, and their diversity exposes the inherent uncertainty in the inverse problem being solved.

Patch Craft: Video Denoising by Deep Modeling and Patch Matching

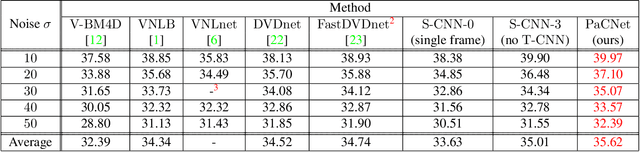
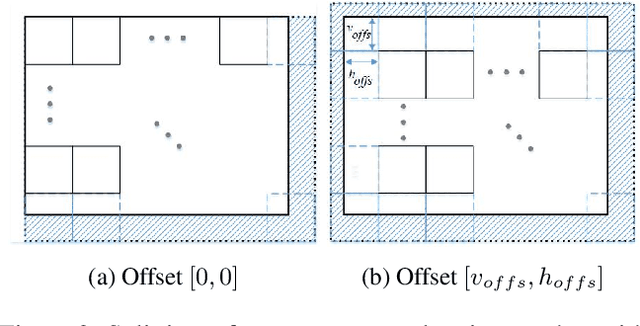
The non-local self-similarity property of natural images has been exploited extensively for solving various image processing problems. When it comes to video sequences, harnessing this force is even more beneficial due to the temporal redundancy. In the context of image and video denoising, many classically-oriented algorithms employ self-similarity, splitting the data into overlapping patches, gathering groups of similar ones and processing these together somehow. With the emergence of convolutional neural networks (CNN), the patch-based framework has been abandoned. Most CNN denoisers operate on the whole image, leveraging non-local relations only implicitly by using a large receptive field. This work proposes a novel approach for leveraging self-similarity in the context of video denoising, while still relying on a regular convolutional architecture. We introduce a concept of patch-craft frames - artificial frames that are similar to the real ones, built by tiling matched patches. Our algorithm augments video sequences with patch-craft frames and feeds them to a CNN. We demonstrate the substantial boost in denoising performance obtained with the proposed approach.

High Perceptual Quality Image Denoising with a Posterior Sampling CGAN

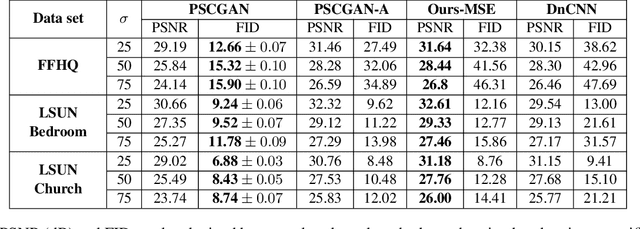
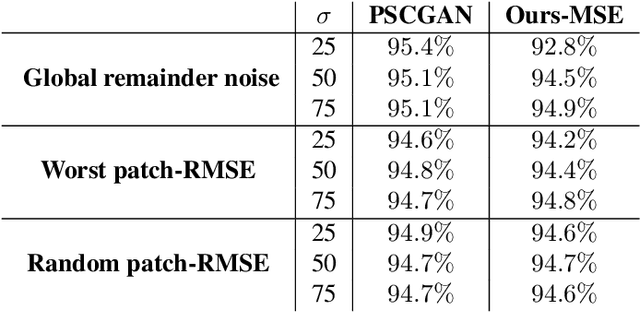
The vast work in Deep Learning (DL) has led to a leap in image denoising research. Most DL solutions for this task have chosen to put their efforts on the denoiser's architecture while maximizing distortion performance. However, distortion driven solutions lead to blurry results with sub-optimal perceptual quality, especially in immoderate noise levels. In this paper we propose a different perspective, aiming to produce sharp and visually pleasing denoised images that are still faithful to their clean sources. Formally, our goal is to achieve high perceptual quality with acceptable distortion. This is attained by a stochastic denoiser that samples from the posterior distribution, trained as a generator in the framework of conditional generative adversarial networks (CGAN). Contrary to distortion-based regularization terms that conflict with perceptual quality, we introduce to the CGAN objective a theoretically founded penalty term that does not force a distortion requirement on individual samples, but rather on their mean. We showcase our proposed method with a novel denoiser architecture that achieves the reformed denoising goal and produces vivid and diverse outcomes in immoderate noise levels.

Stochastic Image Denoising by Sampling from the Posterior Distribution

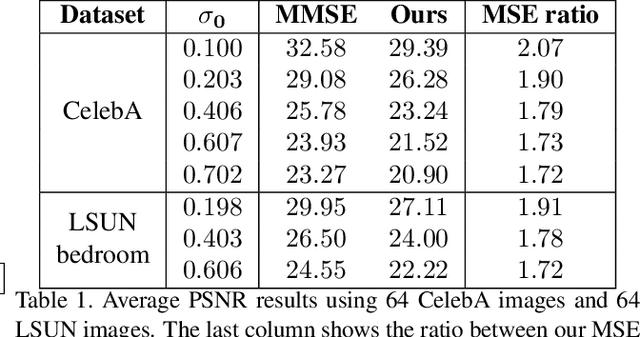
Image denoising is a well-known and well studied problem, commonly targeting a minimization of the mean squared error (MSE) between the outcome and the original image. Unfortunately, especially for severe noise levels, such Minimum MSE (MMSE) solutions may lead to blurry output images. In this work we propose a novel stochastic denoising approach that produces viable and high perceptual quality results, while maintaining a small MSE. Our method employs Langevin dynamics that relies on a repeated application of any given MMSE denoiser, obtaining the reconstructed image by effectively sampling from the posterior distribution. Due to its stochasticity, the proposed algorithm can produce a variety of high-quality outputs for a given noisy input, all shown to be legitimate denoising results. In addition, we present an extension of our algorithm for handling the inpainting problem, recovering missing pixels and removing noise from partially given noisy data.

Low-Weight and Learnable Image Denoising

Image denoising is a well studied problem with an extensive activity that has spread over several decades. Despite the many available denoising algorithms, the quest for simple, powerful and fast denoisers is still an active and vibrant topic of research. Leading classical denoising methods are typically designed to exploit the inner structure in images by modeling local overlapping patches. In contrast, recent newcomers to this arena are supervised neural-network-based methods that bypass this modeling altogether, targeting the inference goal directly and globally, while tending to be very deep and parameter heavy. This work proposes a novel low-weight learnable architecture that embeds in it several of the main concepts from the classical methods, while being trained for best denoising performance. More specifically, our proposed network relies on patch processing, leveraging non-local self-similarity, representation sparsity and a multiscale treatment. The proposed architecture achieves near state-of-the-art denoising results, while using a small fraction of the typical number of parameters. Furthermore, we demonstrate the ability of the proposed network to adapt itself to an incoming image by leveraging similar clean ones.

Patch-Ordering as a Regularization for Inverse Problems in Image Processing

Recent work in image processing suggests that operating on (overlapping) patches in an image may lead to state-of-the-art results. This has been demonstrated for a variety of problems including denoising, inpainting, deblurring, and super-resolution. The work reported in [1,2] takes an extra step forward by showing that ordering these patches to form an approximate shortest path can be leveraged for better processing. The core idea is to apply a simple filter on the resulting 1D smoothed signal obtained after the patch-permutation. This idea has been also explored in combination with a wavelet pyramid, leading eventually to a sophisticated and highly effective regularizer for inverse problems in imaging. In this work we further study the patch-permutation concept, and harness it to propose a new simple yet effective regularization for image restoration problems. Our approach builds on the classic Maximum A'posteriori probability (MAP), with a penalty function consisting of a regular log-likelihood term and a novel permutation-based regularization term. Using a plain 1D Laplacian, the proposed regularization forces robust smoothness (L1) on the permuted pixels. Since the permutation originates from patch-ordering, we propose to accumulate the smoothness terms over all the patches' pixels. Furthermore, we take into account the found distances between adjacent patches in the ordering, by weighting the Laplacian outcome. We demonstrate the proposed scheme on a diverse set of problems: (i) severe Poisson image denoising, (ii) Gaussian image denoising, (iii) image deblurring, and (iv) single image super-resolution. In all these cases, we use recent methods that handle these problems as initialization to our scheme. This is followed by an L-BFGS optimization of the above-described penalty function, leading to state-of-the-art results, and especially so for highly ill-posed cases.