Motif and Hypergraph Correlation Clustering

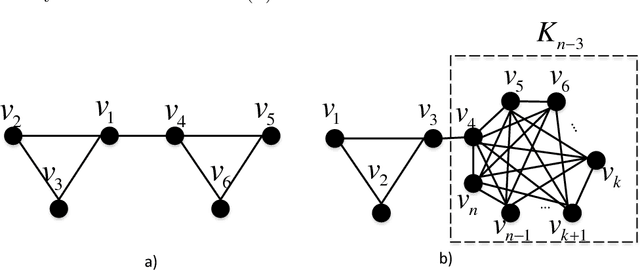
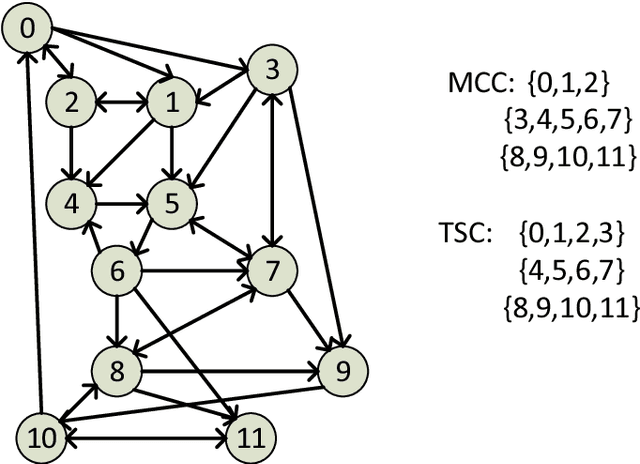
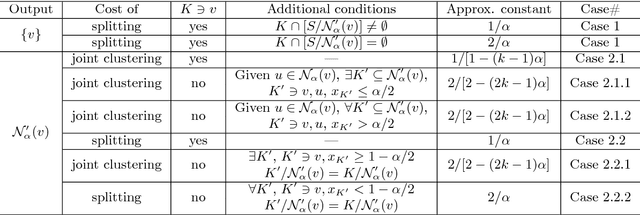
Motivated by applications in social and biological network analysis, we introduce a new form of agnostic clustering termed~\emph{motif correlation clustering}, which aims to minimize the cost of clustering errors associated with both edges and higher-order network structures. The problem may be succinctly described as follows: Given a complete graph $G$, partition the vertices of the graph so that certain predetermined `important' subgraphs mostly lie within the same cluster, while `less relevant' subgraphs are allowed to lie across clusters. Our contributions are as follows: We first introduce several variants of motif correlation clustering and then show that these clustering problems are NP-hard. We then proceed to describe polynomial-time clustering algorithms that provide constant approximation guarantees for the problems at hand. Despite following the frequently used LP relaxation and rounding procedure, the algorithms involve a sophisticated and carefully designed neighborhood growing step that combines information about both edge and motif structures. We conclude with several examples illustrating the performance of the developed algorithms on synthetic and real networks.

Correlation Clustering and Biclustering with Locally Bounded Errors

We consider a generalized version of the correlation clustering problem, defined as follows. Given a complete graph $G$ whose edges are labeled with $+$ or $-$, we wish to partition the graph into clusters while trying to avoid errors: $+$ edges between clusters or $-$ edges within clusters. Classically, one seeks to minimize the total number of such errors. We introduce a new framework that allows the objective to be a more general function of the number of errors at each vertex (for example, we may wish to minimize the number of errors at the worst vertex) and provide a rounding algorithm which converts "fractional clusterings" into discrete clusterings while causing only a constant-factor blowup in the number of errors at each vertex. This rounding algorithm yields constant-factor approximation algorithms for the discrete problem under a wide variety of objective functions.

A new correlation clustering method for cancer mutation analysis

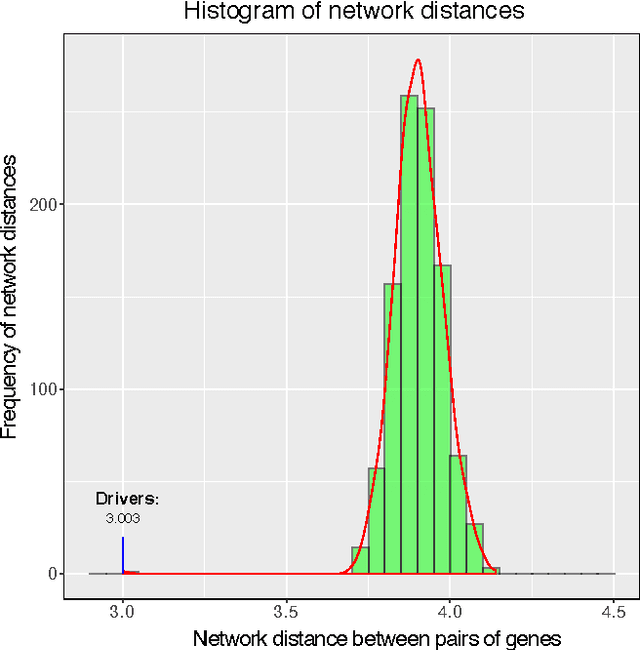
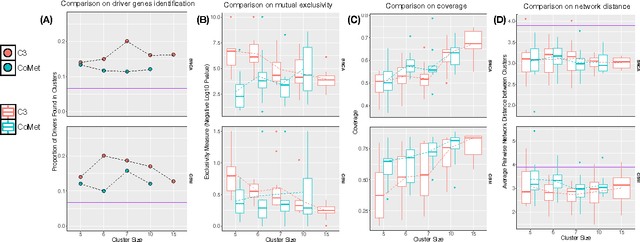
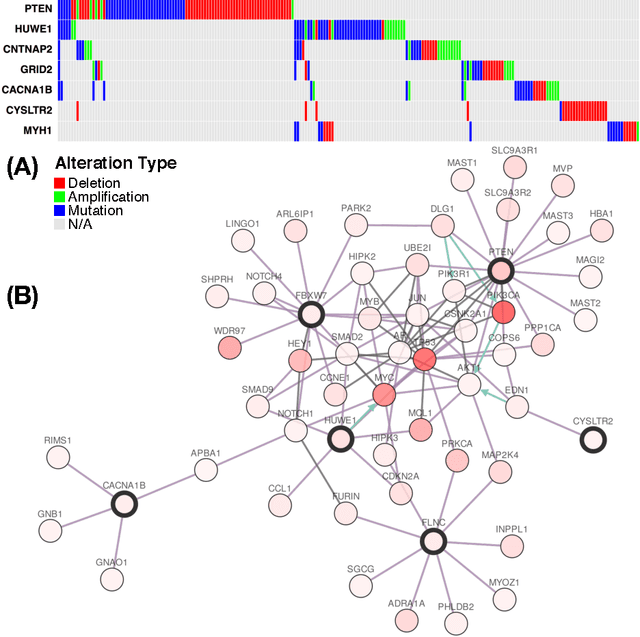
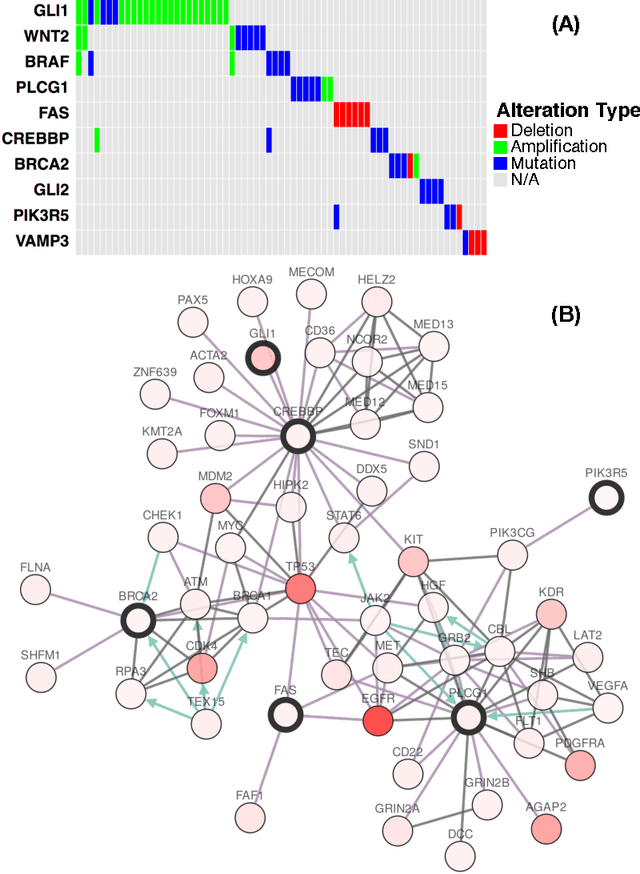
Cancer genomes exhibit a large number of different alterations that affect many genes in a diverse manner. It is widely believed that these alterations follow combinatorial patterns that have a strong connection with the underlying molecular interaction networks and functional pathways. A better understanding of the generative mechanisms behind the mutation rules and their influence on gene communities is of great importance for the process of driver mutations discovery and for identification of network modules related to cancer development and progression. We developed a new method for cancer mutation pattern analysis based on a constrained form of correlation clustering. Correlation clustering is an agnostic learning method that can be used for general community detection problems in which the number of communities or their structure is not known beforehand. The resulting algorithm, named $C^3$, leverages mutual exclusivity of mutations, patient coverage, and driver network concentration principles; it accepts as its input a user determined combination of heterogeneous patient data, such as that available from TCGA (including mutation, copy number, and gene expression information), and creates a large number of clusters containing mutually exclusive mutated genes in a particular type of cancer. The cluster sizes may be required to obey some useful soft size constraints, without impacting the computational complexity of the algorithm. To test $C^3$, we performed a detailed analysis on TCGA breast cancer and glioblastoma data and showed that our algorithm outperforms the state-of-the-art CoMEt method in terms of discovering mutually exclusive gene modules and identifying driver genes. Our $C^3$ method represents a unique tool for efficient and reliable identification of mutation patterns and driver pathways in large-scale cancer genomics studies.

Correlation Clustering with Constrained Cluster Sizes and Extended Weights Bounds

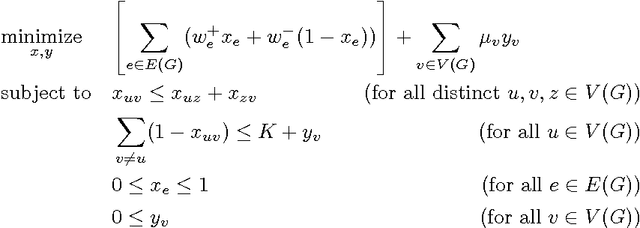
We consider the problem of correlation clustering on graphs with constraints on both the cluster sizes and the positive and negative weights of edges. Our contributions are twofold: First, we introduce the problem of correlation clustering with bounded cluster sizes. Second, we extend the regime of weight values for which the clustering may be performed with constant approximation guarantees in polynomial time and apply the results to the bounded cluster size problem.