Correlation Clustering with Constrained Cluster Sizes and Extended Weights Bounds
Paper and Code
May 22, 2015
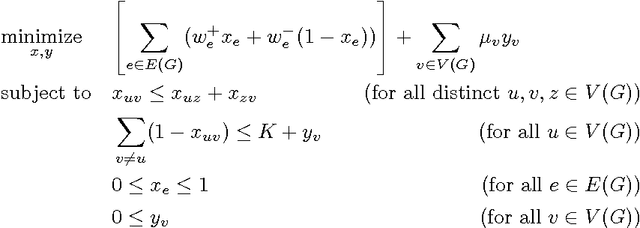

We consider the problem of correlation clustering on graphs with constraints on both the cluster sizes and the positive and negative weights of edges. Our contributions are twofold: First, we introduce the problem of correlation clustering with bounded cluster sizes. Second, we extend the regime of weight values for which the clustering may be performed with constant approximation guarantees in polynomial time and apply the results to the bounded cluster size problem.
* 17 pages, simplified the last section and fixed some other minor
errors
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge