Motif and Hypergraph Correlation Clustering
Paper and Code
Nov 05, 2018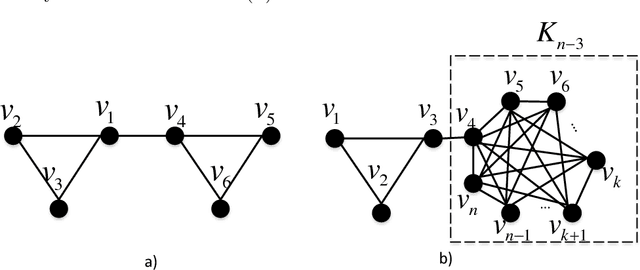

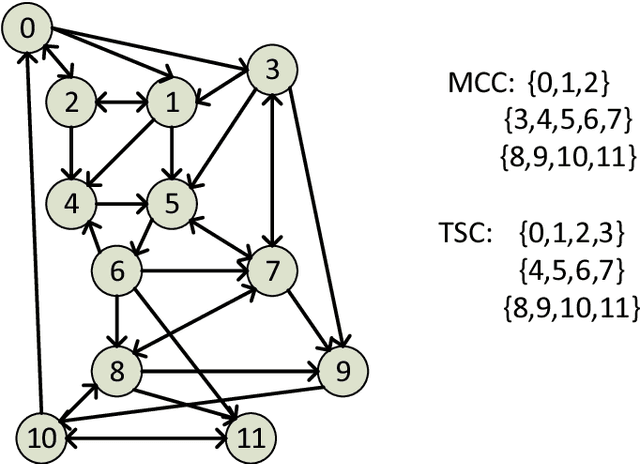
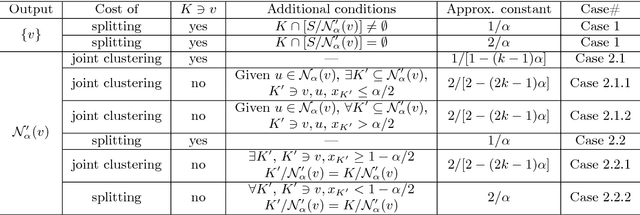
Motivated by applications in social and biological network analysis, we introduce a new form of agnostic clustering termed~\emph{motif correlation clustering}, which aims to minimize the cost of clustering errors associated with both edges and higher-order network structures. The problem may be succinctly described as follows: Given a complete graph $G$, partition the vertices of the graph so that certain predetermined `important' subgraphs mostly lie within the same cluster, while `less relevant' subgraphs are allowed to lie across clusters. Our contributions are as follows: We first introduce several variants of motif correlation clustering and then show that these clustering problems are NP-hard. We then proceed to describe polynomial-time clustering algorithms that provide constant approximation guarantees for the problems at hand. Despite following the frequently used LP relaxation and rounding procedure, the algorithms involve a sophisticated and carefully designed neighborhood growing step that combines information about both edge and motif structures. We conclude with several examples illustrating the performance of the developed algorithms on synthetic and real networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge