Sparse Regression for Discovery of Constitutive Models from Oscillatory Shear Measurements

We propose sparse regression as an alternative to neural networks for the discovery of parsimonious constitutive models (CMs) from oscillatory shear experiments. Symmetry and frame-invariance are strictly imposed by using tensor basis functions to isolate and describe unknown nonlinear terms in the CMs. We generate synthetic experimental data using the Giesekus and Phan-Thien Tanner CMs, and consider two different scenarios. In the complete information scenario, we assume that the shear stress, along with the first and second normal stress differences, is measured. This leads to a sparse linear regression problem that can be solved efficiently using $l_1$ regularization. In the partial information scenario, we assume that only shear stress data is available. This leads to a more challenging sparse nonlinear regression problem, for which we propose a greedy two-stage algorithm. In both scenarios, the proposed methods fit and interpolate the training data remarkably well. Predictions of the inferred CMs extrapolate satisfactorily beyond the range of training data for oscillatory shear. They also extrapolate reasonably well to flow conditions like startup of steady and uniaxial extension that are not used in the identification of CMs. We discuss ramifications for experimental design, potential algorithmic improvements, and implications of the non-uniqueness of CMs inferred from partial information.

The Generalization-Stability Tradeoff in Neural Network Pruning

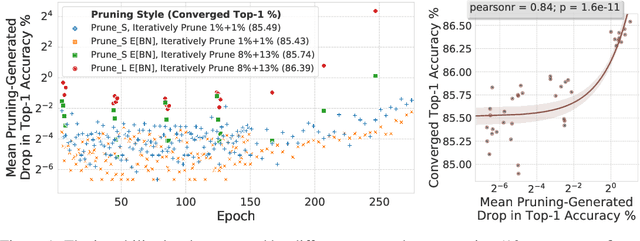
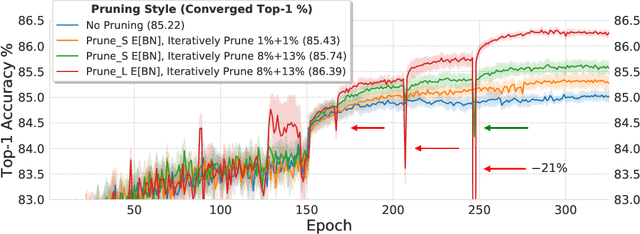
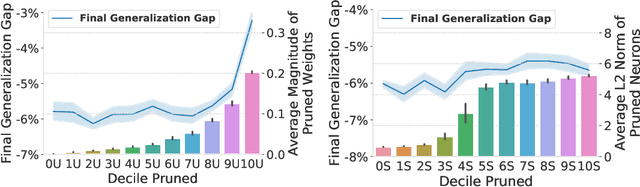
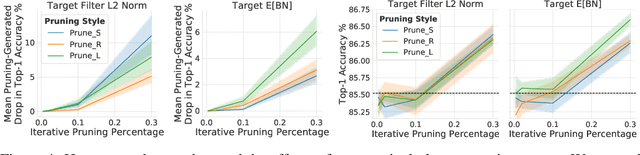
Pruning neural network parameters to reduce model size is an area of much interest, but the original motivation for pruning was the prevention of overfitting rather than the improvement of computational efficiency. This motivation is particularly relevant given the perhaps surprising observation that a wide variety of pruning approaches confer increases in test accuracy, even when parameter counts are drastically reduced. To better understand this phenomenon, we analyze the behavior of pruning over the course of training, finding that pruning's effect on generalization relies more on the instability generated by pruning than the final size of the pruned model. We demonstrate that even pruning of seemingly unimportant parameters can lead to such instability, allowing our finding to account for the generalization benefits of modern pruning techniques. Our results ultimately suggest that, counter-intuitively, pruning regularizes through instability and mechanisms unrelated to parameter counts.

Enhancing the Regularization Effect of Weight Pruning in Artificial Neural Networks

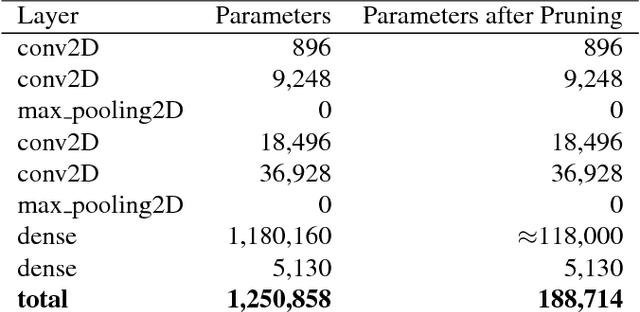
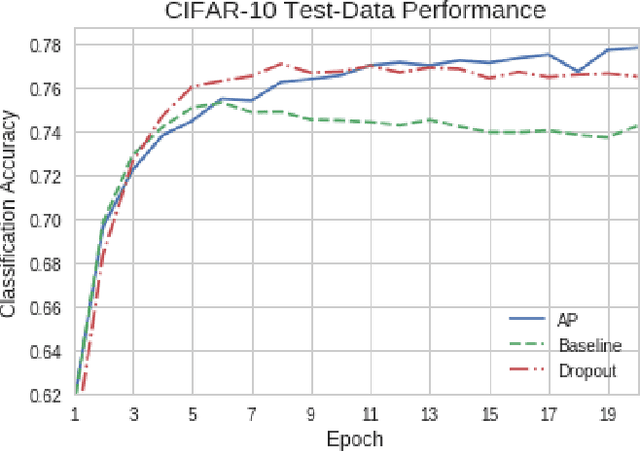
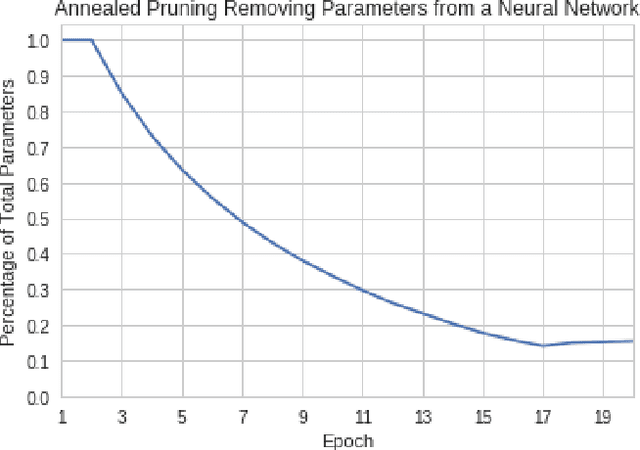
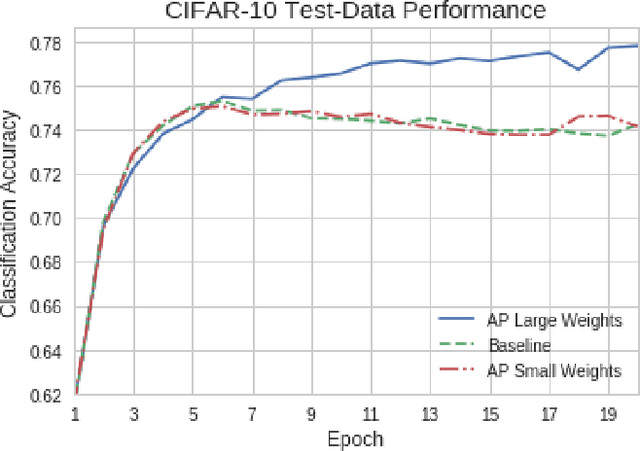
Artificial neural networks (ANNs) may not be worth their computational/memory costs when used in mobile phones or embedded devices. Parameter-pruning algorithms combat these costs, with some algorithms capable of removing over 90% of an ANN's weights without harming the ANN's performance. Removing weights from an ANN is a form of regularization, but existing pruning algorithms do not significantly improve generalization error. We show that pruning ANNs can improve generalization if pruning targets large weights instead of small weights. Applying our pruning algorithm to an ANN leads to a higher image classification accuracy on CIFAR-10 data than applying the popular regularizer dropout. The pruning couples this higher accuracy with an 85% reduction of the ANN's parameter count.