Semi-Supervised Constrained Clustering: An In-Depth Overview, Ranked Taxonomy and Future Research Directions

Clustering is a well-known unsupervised machine learning approach capable of automatically grouping discrete sets of instances with similar characteristics. Constrained clustering is a semi-supervised extension to this process that can be used when expert knowledge is available to indicate constraints that can be exploited. Well-known examples of such constraints are must-link (indicating that two instances belong to the same group) and cannot-link (two instances definitely do not belong together). The research area of constrained clustering has grown significantly over the years with a large variety of new algorithms and more advanced types of constraints being proposed. However, no unifying overview is available to easily understand the wide variety of available methods, constraints and benchmarks. To remedy this, this study presents in-detail the background of constrained clustering and provides a novel ranked taxonomy of the types of constraints that can be used in constrained clustering. In addition, it focuses on the instance-level pairwise constraints, and gives an overview of its applications and its historical context. Finally, it presents a statistical analysis covering 307 constrained clustering methods, categorizes them according to their features, and provides a ranking score indicating which methods have the most potential based on their popularity and validation quality. Finally, based upon this analysis, potential pitfalls and future research directions are provided.

Semi-supervised Clustering with Two Types of Background Knowledge: Fusing Pairwise Constraints and Monotonicity Constraints

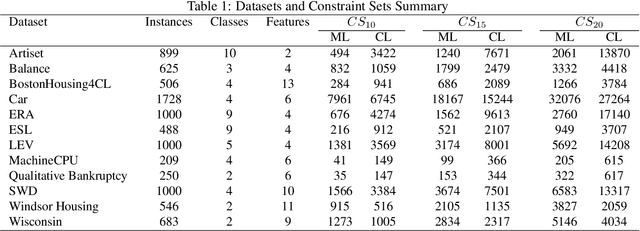
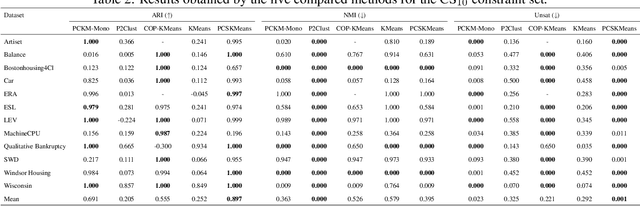
This study addresses the problem of performing clustering in the presence of two types of background knowledge: pairwise constraints and monotonicity constraints. To achieve this, the formal framework to perform clustering under monotonicity constraints is, firstly, defined, resulting in a specific distance measure. Pairwise constraints are integrated afterwards by designing an objective function which combines the proposed distance measure and a pairwise constraint-based penalty term, in order to fuse both types of information. This objective function can be optimized with an EM optimization scheme. The proposed method serves as the first approach to the problem it addresses, as it is the first method designed to work with the two types of background knowledge mentioned above. Our proposal is tested in a variety of benchmark datasets and in a real-world case of study.