Semi-supervised Clustering with Two Types of Background Knowledge: Fusing Pairwise Constraints and Monotonicity Constraints

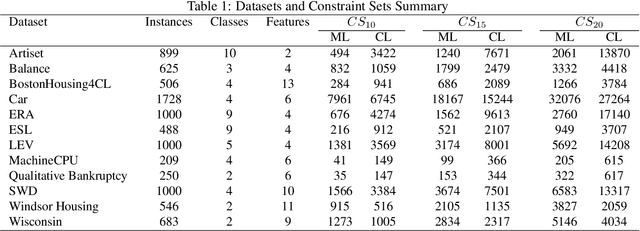
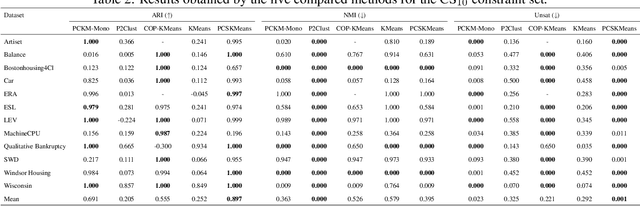
This study addresses the problem of performing clustering in the presence of two types of background knowledge: pairwise constraints and monotonicity constraints. To achieve this, the formal framework to perform clustering under monotonicity constraints is, firstly, defined, resulting in a specific distance measure. Pairwise constraints are integrated afterwards by designing an objective function which combines the proposed distance measure and a pairwise constraint-based penalty term, in order to fuse both types of information. This objective function can be optimized with an EM optimization scheme. The proposed method serves as the first approach to the problem it addresses, as it is the first method designed to work with the two types of background knowledge mentioned above. Our proposal is tested in a variety of benchmark datasets and in a real-world case of study.

A Tutorial on Distance Metric Learning: Mathematical Foundations, Algorithms and Software

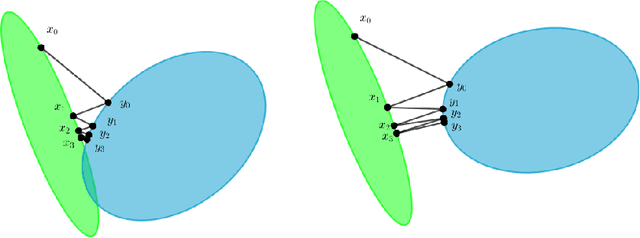
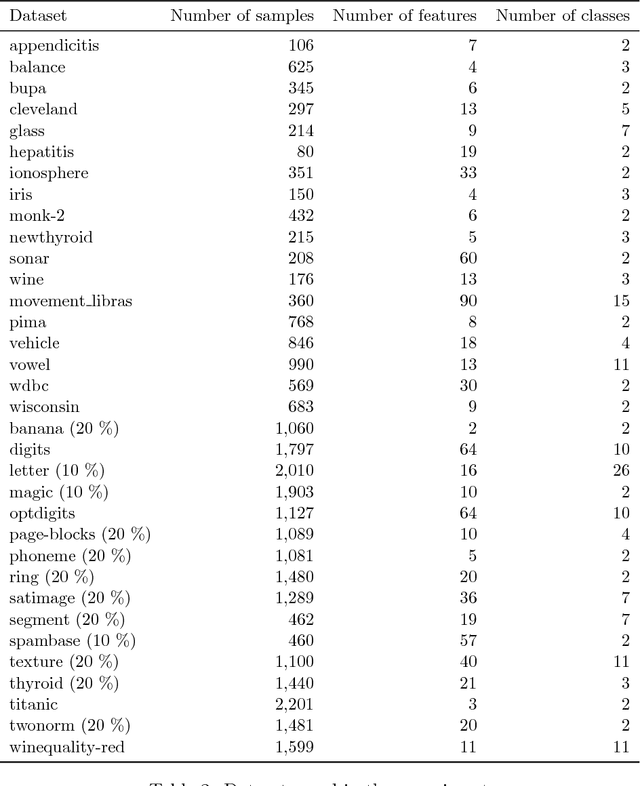
This paper describes the discipline of distance metric learning, a branch of machine learning that aims to learn distances from the data. Distance metric learning can be useful to improve similarity learning algorithms, and also has applications in dimensionality reduction. We describe the distance metric learning problem and analyze its main mathematical foundations. We discuss some of the most popular distance metric learning techniques used in classification, showing their goals and the required information to understand and use them. Furthermore, we present a Python package that collects a set of 17 distance metric learning techniques explained in this paper, with some experiments to evaluate the performance of the different algorithms. Finally, we discuss several possibilities of future work in this topic.