SorryDB: Can AI Provers Complete Real-World Lean Theorems?

We present SorryDB, a dynamically-updating benchmark of open Lean tasks drawn from 78 real world formalization projects on GitHub. Unlike existing static benchmarks, often composed of competition problems, hillclimbing the SorryDB benchmark will yield tools that are aligned to the community needs, more usable by mathematicians, and more capable of understanding complex dependencies. Moreover, by providing a continuously updated stream of tasks, SorryDB mitigates test-set contamination and offers a robust metric for an agent's ability to contribute to novel formal mathematics projects. We evaluate a collection of approaches, including generalist large language models, agentic approaches, and specialized symbolic provers, over a selected snapshot of 1000 tasks from SorryDB. We show that current approaches are complementary: even though an agentic approach based on Gemini Flash is the most performant, it is not strictly better than other off-the-shelf large-language models, specialized provers, or even a curated list of Lean tactics.

Learning Interestingness in Automated Mathematical Theory Formation

We take two key steps in automating the open-ended discovery of new mathematical theories, a grand challenge in artificial intelligence. First, we introduce $\emph{FERMAT}$, a reinforcement learning (RL) environment that models concept discovery and theorem-proving using a set of symbolic actions, opening up a range of RL problems relevant to theory discovery. Second, we explore a specific problem through $\emph{FERMAT}$: automatically scoring the $\emph{interestingness}$ of mathematical objects. We investigate evolutionary algorithms for synthesizing nontrivial interestingness measures. In particular, we introduce an LLM-based evolutionary algorithm that features function abstraction, leading to notable improvements in discovering elementary number theory and finite fields over hard-coded baselines. We open-source the $\emph{FERMAT}$ environment at this URL(https://github.com/trishullab/Fermat).

CLEVER: A Curated Benchmark for Formally Verified Code Generation

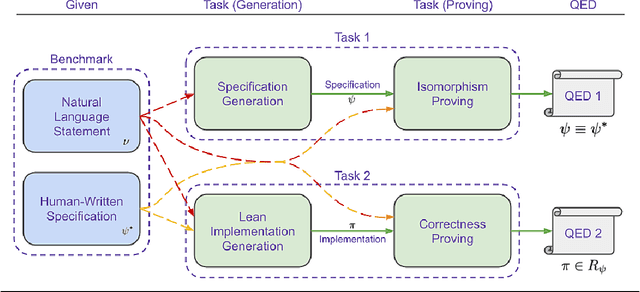
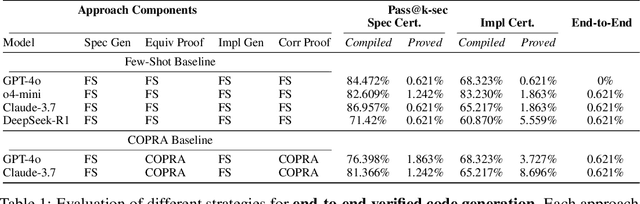
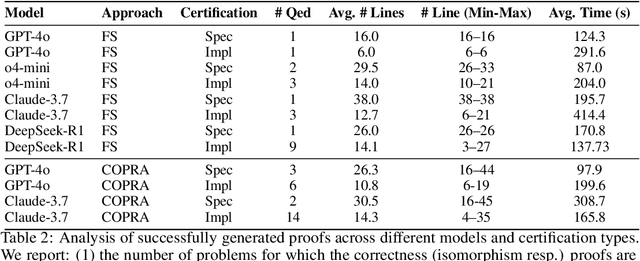
We introduce ${\rm C{\small LEVER}}$, a high-quality, curated benchmark of 161 problems for end-to-end verified code generation in Lean. Each problem consists of (1) the task of generating a specification that matches a held-out ground-truth specification, and (2) the task of generating a Lean implementation that provably satisfies this specification. Unlike prior benchmarks, ${\rm C{\small LEVER}}$ avoids test-case supervision, LLM-generated annotations, and specifications that leak implementation logic or allow vacuous solutions. All outputs are verified post-hoc using Lean's type checker to ensure machine-checkable correctness. We use ${\rm C{\small LEVER}}$ to evaluate several few-shot and agentic approaches based on state-of-the-art language models. These methods all struggle to achieve full verification, establishing it as a challenging frontier benchmark for program synthesis and formal reasoning. Our benchmark can be found on GitHub(https://github.com/trishullab/clever) as well as HuggingFace(https://huggingface.co/datasets/amitayusht/clever). All our evaluation code is also available online(https://github.com/trishullab/clever-prover).

${\rm P{\small ROOF}W{\small ALA}}$: Multilingual Proof Data Synthesis and Theorem-Proving

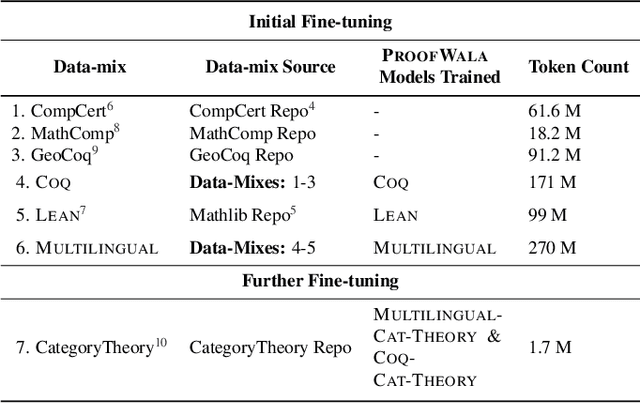
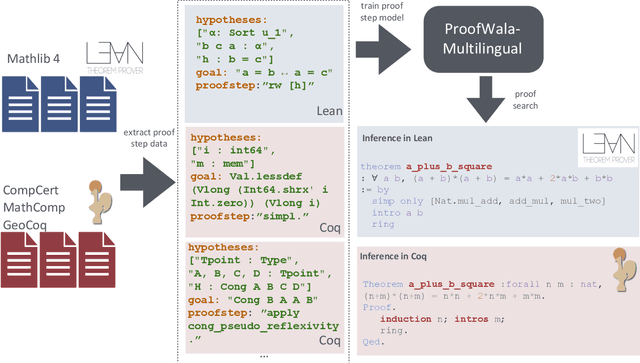
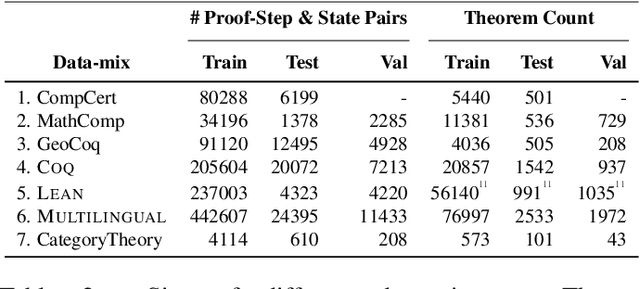
Neural networks have shown substantial promise at automatic theorem-proving in interactive proof assistants (ITPs) like Lean and Coq. However, most neural theorem-proving models are restricted to specific ITPs, leaving out opportunities for cross-lingual $\textit{transfer}$ between ITPs. We address this weakness with a multilingual proof framework, ${\rm P{\small ROOF}W{\small ALA}}$, that allows a standardized form of interaction between neural theorem-provers and two established ITPs (Coq and Lean). It enables the collection of multilingual proof step data -- data recording the result of proof actions on ITP states -- for training neural provers. ${\rm P{\small ROOF}W{\small ALA}}$ allows the systematic evaluation of a model's performance across different ITPs and problem domains via efficient parallel proof search algorithms. We show that multilingual training enabled by ${\rm P{\small ROOF}W{\small ALA}}$ can lead to successful transfer across ITPs. Specifically, a model trained on a mix of ${\rm P{\small ROOF}W{\small ALA}}$-generated Coq and Lean data outperforms Lean-only and Coq-only models on the standard prove-at-$k$ metric. We open source all code including code for the $\href{https://github.com/trishullab/proof-wala}{ProofWala\; Framework}$, and the $\href{https://github.com/trishullab/itp-interface}{Multilingual\; ITP\; interaction\; framework}$.

PutnamBench: Evaluating Neural Theorem-Provers on the Putnam Mathematical Competition

We present PutnamBench, a new multilingual benchmark for evaluating the ability of neural theorem-provers to solve competition mathematics problems. PutnamBench consists of 1697 hand-constructed formalizations of 640 theorems sourced from the William Lowell Putnam Mathematical Competition, the premier undergraduate-level mathematics competition in North America. All the theorems have formalizations in Lean 4 and Isabelle; a substantial subset also has Coq formalizations. Proving the theorems requires significant problem-solving ability and proficiency in a broad range of topics taught in undergraduate mathematics courses. We use PutnamBench to evaluate several established neural and symbolic theorem-provers. These approaches can only solve a handful of the PutnamBench problems, establishing the benchmark as a difficult open challenge for research on neural theorem-proving. PutnamBench is available at https://github.com/trishullab/PutnamBench.