On Query-efficient Planning in MDPs under Linear Realizability of the Optimal State-value Function

We consider the problem of local planning in fixed-horizon Markov Decision Processes (MDPs) with a generative model under the assumption that the optimal value function lies in the span of a feature map that is accessible through the generative model. As opposed to previous work where linear realizability of all policies was assumed, we consider the significantly relaxed assumption of a single linearly realizable (deterministic) policy. A recent lower bound established that the related problem when the action-value function of the optimal policy is linearly realizable requires an exponential number of queries, either in H (the horizon of the MDP) or d (the dimension of the feature mapping). Their construction crucially relies on having an exponentially large action set. In contrast, in this work, we establish that poly$(H, d)$ learning is possible (with state value function realizability) whenever the action set is small (i.e. O(1)). In particular, we present the TensorPlan algorithm which uses poly$((dH/\delta)^A)$ queries to find a $\delta$-optimal policy relative to any deterministic policy for which the value function is linearly realizable with a parameter from a fixed radius ball around zero. This is the first algorithm to give a polynomial query complexity guarantee using only linear-realizability of a single competing value function. Whether the computation cost is similarly bounded remains an interesting open question. The upper bound is complemented by a lower bound which proves that in the infinite-horizon episodic setting, planners that achieve constant suboptimality need exponentially many queries, either in the dimension or the number of actions.

Exponential Lower Bounds for Planning in MDPs With Linearly-Realizable Optimal Action-Value Functions

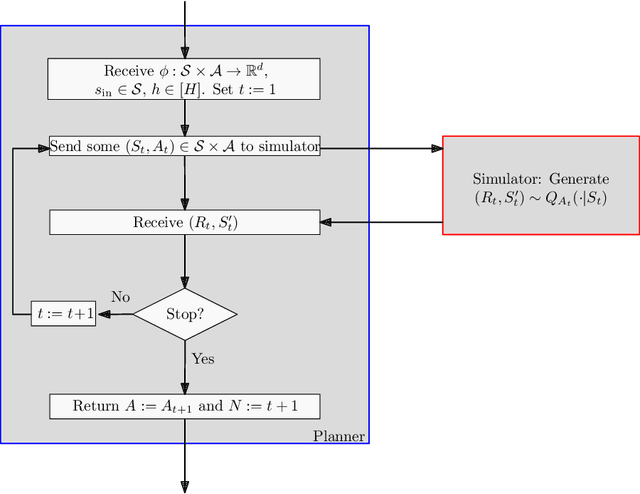
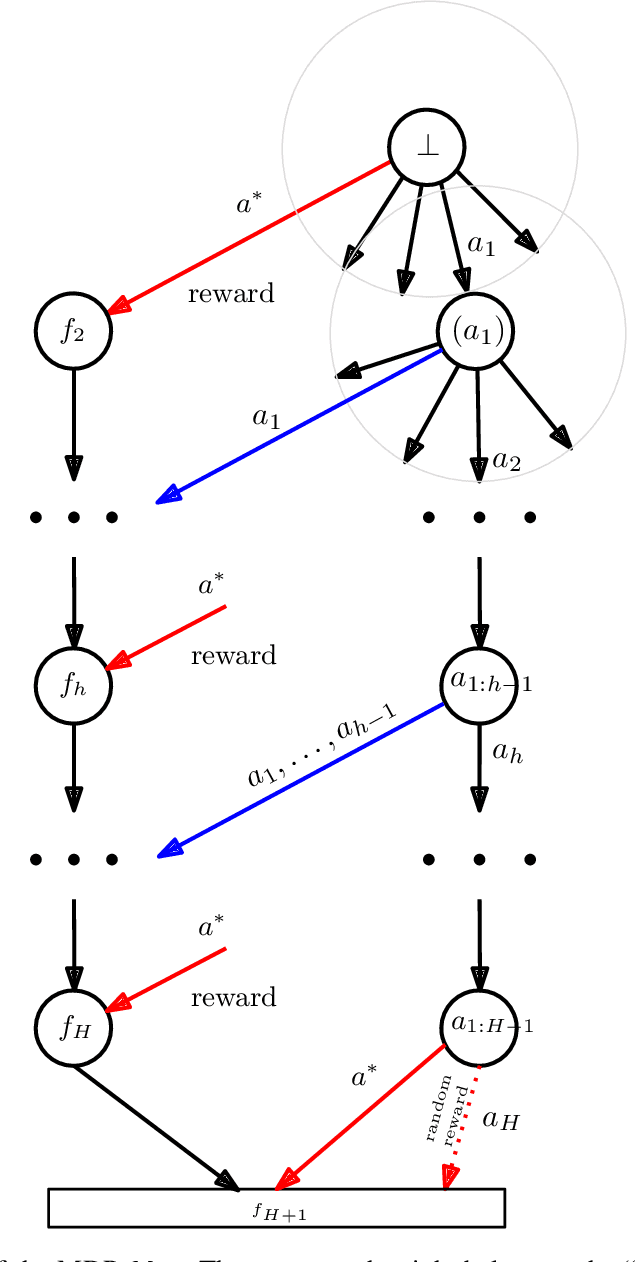
We consider the problem of local planning in fixed-horizon Markov Decision Processes (MDPs) with linear function approximation and a generative model under the assumption that the optimal action-value function lies in the span of a feature map that is available to the planner. Previous work has left open the question of whether there exists sound planners that need only poly(H, d) queries regardless of the MDP, where H is the horizon and d is the dimensionality of the features. We answer this question in the negative: we show that any sound planner must query at least min(exp({\Omega}(d)), {\Omega}(2^H)) samples. We also show that for any {\delta}>0, the least-squares value iteration algorithm with O(H^5d^(H+1)/{\delta}^2) queries can compute a {\delta}-optimal policy. We discuss implications and remaining open questions.

Exploration-Enhanced POLITEX

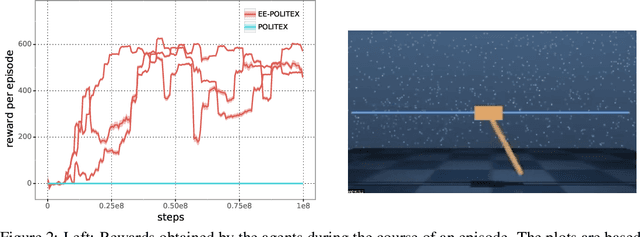
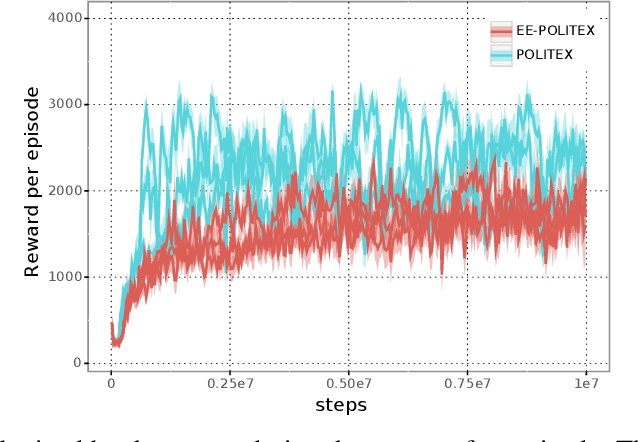
We study algorithms for average-cost reinforcement learning problems with value function approximation. Our starting point is the recently proposed POLITEX algorithm, a version of policy iteration where the policy produced in each iteration is near-optimal in hindsight for the sum of all past value function estimates. POLITEX has sublinear regret guarantees in uniformly-mixing MDPs when the value estimation error can be controlled, which can be satisfied if all policies sufficiently explore the environment. Unfortunately, this assumption is often unrealistic. Motivated by the rapid growth of interest in developing policies that learn to explore their environment in the lack of rewards (also known as no-reward learning), we replace the previous assumption that all policies explore the environment with that a single, sufficiently exploring policy is available beforehand. The main contribution of the paper is the modification of POLITEX to incorporate such an exploration policy in a way that allows us to obtain a regret guarantee similar to the previous one but without requiring that all policies explore environment. In addition to the novel theoretical guarantees, we demonstrate the benefits of our scheme on environments which are difficult to explore using simple schemes like dithering. While the solution we obtain may not achieve the best possible regret, it is the first result that shows how to control the regret in the presence of function approximation errors on problems where exploration is nontrivial. Our approach can also be seen as a way of reducing the problem of minimizing the regret to learning a good exploration policy. We believe that modular approaches like ours can be highly beneficial in tackling harder control problems.