Model Predictive Control with Visibility Graphs for Humanoid Path Planning and Tracking Against Adversarial Opponents

In this paper we detail the methods used for obstacle avoidance, path planning, and trajectory tracking that helped us win the adult-sized, autonomous humanoid soccer league in RoboCup 2024. Our team was undefeated for all seated matches and scored 45 goals over 6 games, winning the championship game 6 to 1. During the competition, a major challenge for collision avoidance was the measurement noise coming from bipedal locomotion and a limited field of view (FOV). Furthermore, obstacles would sporadically jump in and out of our planned trajectory. At times our estimator would place our robot inside a hard constraint. Any planner in this competition must also be be computationally efficient enough to re-plan and react in real time. This motivated our approach to trajectory generation and tracking. In many scenarios long-term and short-term planning is needed. To efficiently find a long-term general path that avoids all obstacles we developed DAVG (Dynamic Augmented Visibility Graphs). DAVG focuses on essential path planning by setting certain regions to be active based on obstacles and the desired goal pose. By augmenting the states in the graph, turning angles are considered, which is crucial for a large soccer playing robot as turning may be more costly. A trajectory is formed by linearly interpolating between discrete points generated by DAVG. A modified version of model predictive control (MPC) is used to then track this trajectory called cf-MPC (Collision-Free MPC). This ensures short-term planning. Without having to switch formulations cf-MPC takes into account the robot dynamics and collision free constraints. Without a hard switch the control input can smoothly transition in cases where the noise places our robot inside a constraint boundary. The nonlinear formulation runs at approximately 120 Hz, while the quadratic version achieves around 400 Hz.

Fast and Robust Localization for Humanoid Soccer Robot via Iterative Landmark Matching

Accurate robot localization is essential for effective operation. Monte Carlo Localization (MCL) is commonly used with known maps but is computationally expensive due to landmark matching for each particle. Humanoid robots face additional challenges, including sensor noise from locomotion vibrations and a limited field of view (FOV) due to camera placement. This paper proposes a fast and robust localization method via iterative landmark matching (ILM) for humanoid robots. The iterative matching process improves the accuracy of the landmark association so that it does not need MCL to match landmarks to particles. Pose estimation with the outlier removal process enhances its robustness to measurement noise and faulty detections. Furthermore, an additional filter can be utilized to fuse inertial data from the inertial measurement unit (IMU) and pose data from localization. We compared ILM with Iterative Closest Point (ICP), which shows that ILM method is more robust towards the error in the initial guess and easier to get a correct matching. We also compared ILM with the Augmented Monte Carlo Localization (aMCL), which shows that ILM method is much faster than aMCL and even more accurate. The proposed method's effectiveness is thoroughly evaluated through experiments and validated on the humanoid robot ARTEMIS during RoboCup 2024 adult-sized soccer competition.

Benchmark Results for Bookshelf Organization Problem as Mixed Integer Nonlinear Program with Mode Switch and Collision Avoidance

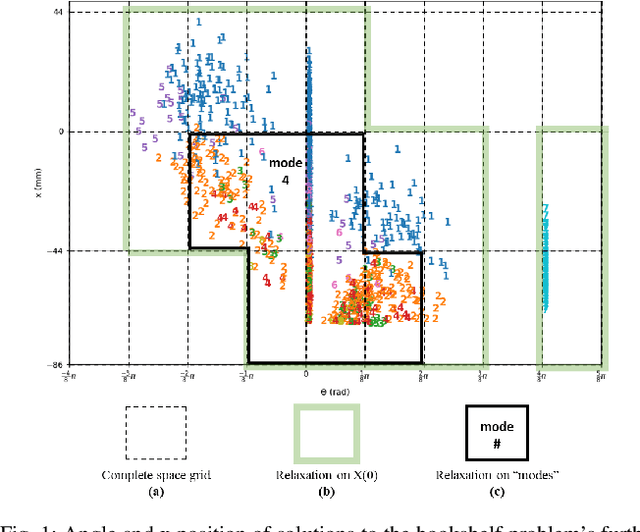
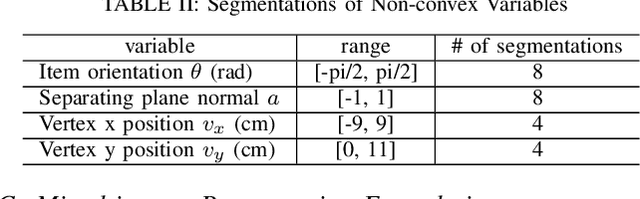
Mixed integer convex and nonlinear programs, MICP and MINLP, are expressive but require long solving times. Recent work that combines data-driven methods on solver heuristics has shown potential to overcome this issue allowing for applications on larger scale practical problems. To solve mixed-integer bilinear programs online with data-driven methods, several formulations exist including mathematical programming with complementary constraints (MPCC), mixed-integer programming (MIP). In this work, we benchmark the performances of those data-driven schemes on a bookshelf organization problem that has discrete mode switch and collision avoidance constraints. The success rate, optimal cost and solving time are compared along with non-data-driven methods. Our proposed methods are demonstrated as a high level planner for a robotic arm for the bookshelf problem.

Feasibility Study of LIMMS, A Multi-Agent Modular Robotic Delivery System with Various Locomotion and Manipulation Modes

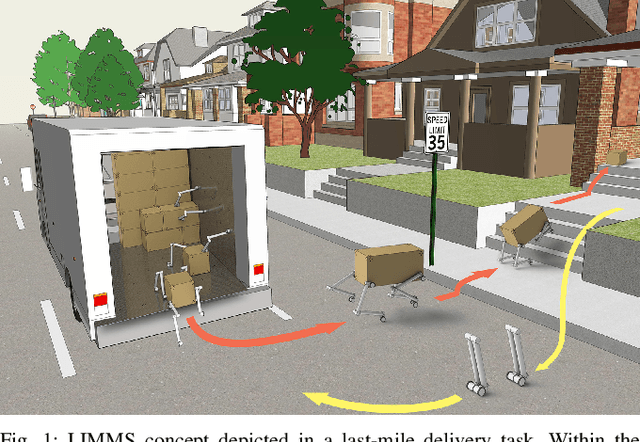
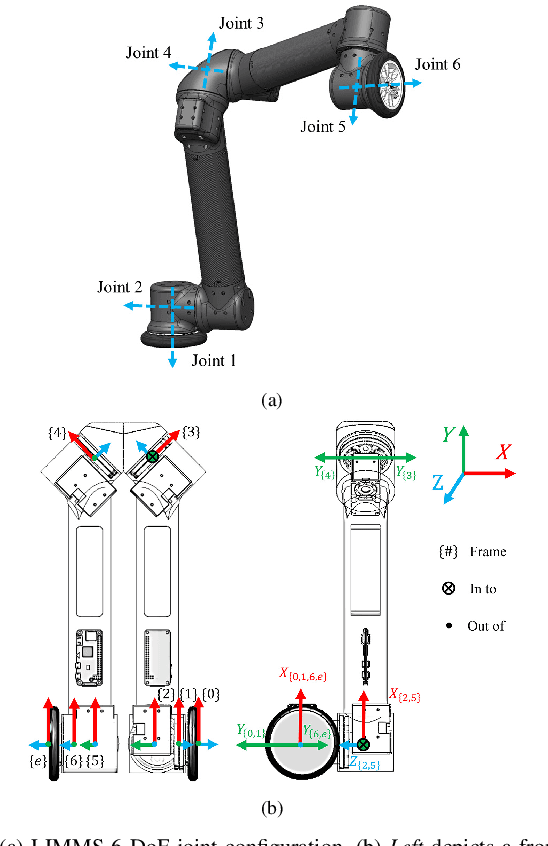
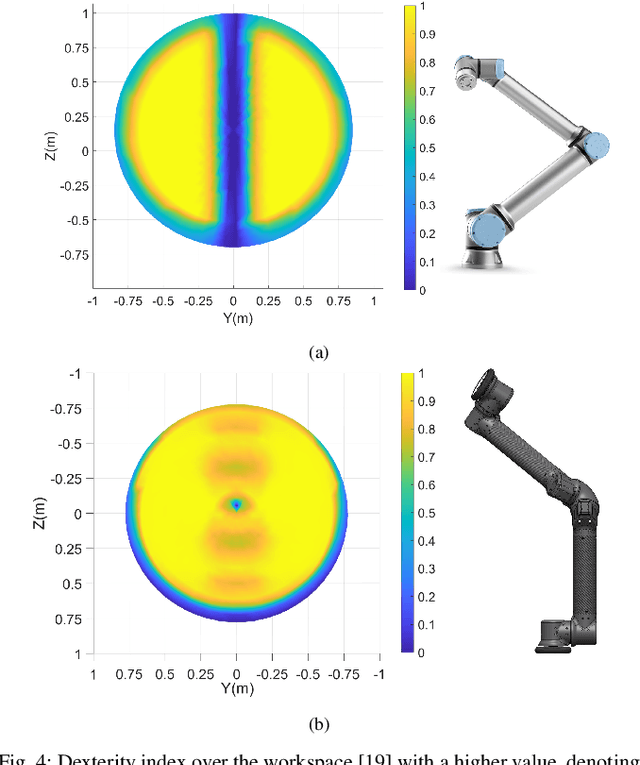
The logistics of transporting a package from a storage facility to the consumer's front door usually employs highly specialized robots often times splitting sub-tasks up to different systems, e.g., manipulator arms to sort and wheeled vehicles to deliver. More recent endeavors attempt to have a unified approach with legged and humanoid robots. These solutions, however, occupy large amounts of space thus reducing the number of packages that can fit into a delivery vehicle. As a result, these bulky robotic systems often reduce the potential for scalability and task parallelization. In this paper, we introduce LIMMS (Latching Intelligent Modular Mobility System) to address both the manipulation and delivery portion of a typical last-mile delivery while maintaining a minimal spatial footprint. LIMMS is a symmetrically designed, 6 degree of freedom (DoF) appendage-like robot with wheels and latching mechanisms at both ends. By latching onto a surface and anchoring at one end, LIMMS can function as a traditional 6-DoF manipulator arm. On the other hand, multiple LIMMS can latch onto a single box and behave like a legged robotic system where the package is the body. During transit, LIMMS folds up compactly and takes up much less space compared to traditional robotic systems. A large group of LIMMS units can fit inside of a single delivery vehicle, opening the potential for new delivery optimization and hybrid planning methods never done before. In this paper, the feasibility of LIMMS is studied and presented using a hardware prototype as well as simulation results for a range of sub-tasks in a typical last-mile delivery.

ReDUCE: Reformulation of Mixed Integer Programs using Data from Unsupervised Clusters for Learning Efficient Strategies

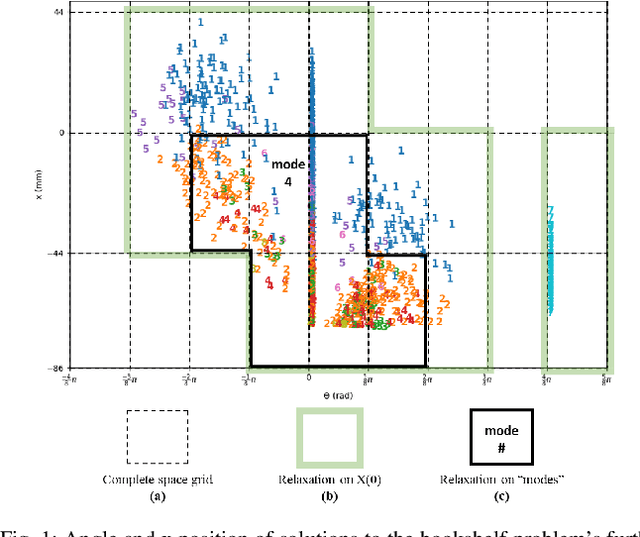
Mixed integer convex and nonlinear programs, MICP and MINLP, are expressive but require long solving times. Recent work that combines learning methods on solver heuristics has shown potential to overcome this issue allowing for applications on larger scale practical problems. Gathering sufficient training data to employ these methods still present a challenge since getting data from traditional solvers are slow and newer learning approaches still require large amounts of data. In order to scale up and make these hybrid learning approaches more manageable we propose ReDUCE, a method that exploits structure within small to medium size datasets. We also introduce the bookshelf organization problem as an MINLP as a way to measure performance of solvers with ReDUCE. Results show that existing algorithms with ReDUCE can solve this problem within a few seconds, a significant improvement over the original formulation. ReDUCE is demonstrated as a high level planner for a robotic arm for the bookshelf problem.

Deep Reinforcement Learning with Linear Quadratic Regulator Regions

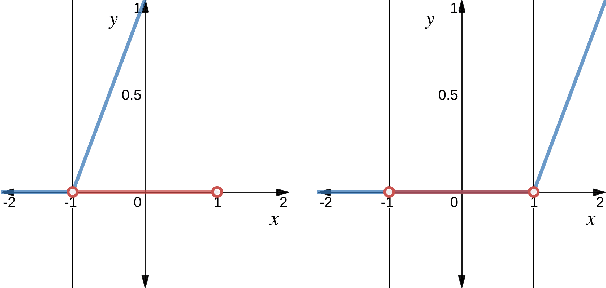
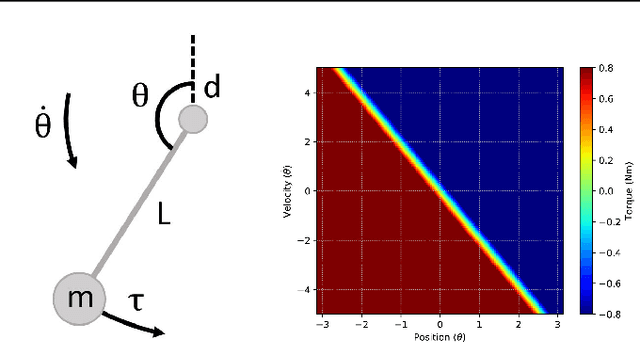
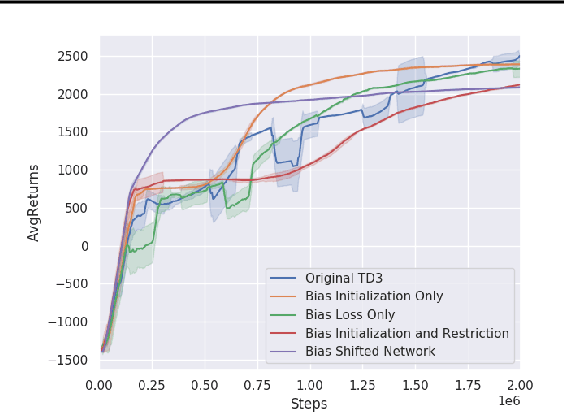
Practitioners often rely on compute-intensive domain randomization to ensure reinforcement learning policies trained in simulation can robustly transfer to the real world. Due to unmodeled nonlinearities in the real system, however, even such simulated policies can still fail to perform stably enough to acquire experience in real environments. In this paper we propose a novel method that guarantees a stable region of attraction for the output of a policy trained in simulation, even for highly nonlinear systems. Our core technique is to use "bias-shifted" neural networks for constructing the controller and training the network in the simulator. The modified neural networks not only capture the nonlinearities of the system but also provably preserve linearity in a certain region of the state space and thus can be tuned to resemble a linear quadratic regulator that is known to be stable for the real system. We have tested our new method by transferring simulated policies for a swing-up inverted pendulum to real systems and demonstrated its efficacy.