Deep Reinforcement Learning with Linear Quadratic Regulator Regions
Paper and Code
Feb 26, 2020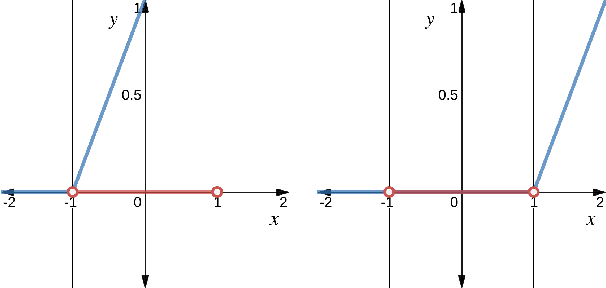

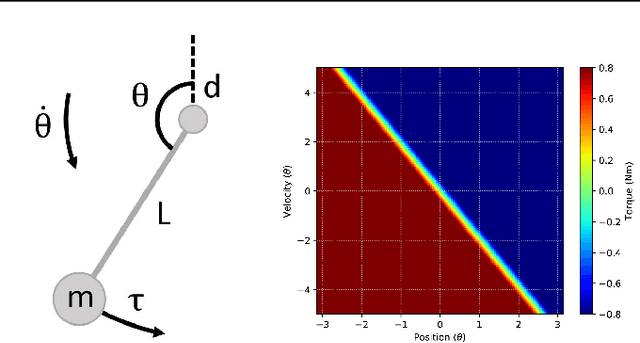
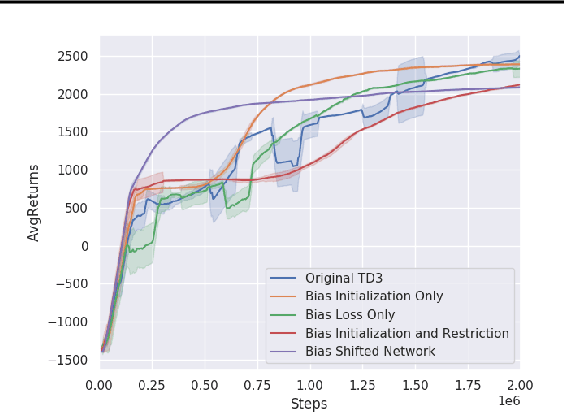
Practitioners often rely on compute-intensive domain randomization to ensure reinforcement learning policies trained in simulation can robustly transfer to the real world. Due to unmodeled nonlinearities in the real system, however, even such simulated policies can still fail to perform stably enough to acquire experience in real environments. In this paper we propose a novel method that guarantees a stable region of attraction for the output of a policy trained in simulation, even for highly nonlinear systems. Our core technique is to use "bias-shifted" neural networks for constructing the controller and training the network in the simulator. The modified neural networks not only capture the nonlinearities of the system but also provably preserve linearity in a certain region of the state space and thus can be tuned to resemble a linear quadratic regulator that is known to be stable for the real system. We have tested our new method by transferring simulated policies for a swing-up inverted pendulum to real systems and demonstrated its efficacy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge