Colin Togashi
A Hierarchical, Model-Based System for High-Performance Humanoid Soccer
Dec 10, 2025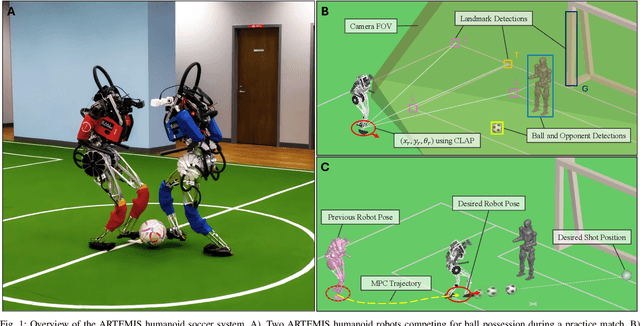

Abstract:The development of athletic humanoid robots has gained significant attention as advances in actuation, sensing, and control enable increasingly dynamic, real-world capabilities. RoboCup, an international competition of fully autonomous humanoid robots, provides a uniquely challenging benchmark for such systems, culminating in the long-term goal of competing against human soccer players by 2050. This paper presents the hardware and software innovations underlying our team's victory in the RoboCup 2024 Adult-Sized Humanoid Soccer Competition. On the hardware side, we introduce an adult-sized humanoid platform built with lightweight structural components, high-torque quasi-direct-drive actuators, and a specialized foot design that enables powerful in-gait kicks while preserving locomotion robustness. On the software side, we develop an integrated perception and localization framework that combines stereo vision, object detection, and landmark-based fusion to provide reliable estimates of the ball, goals, teammates, and opponents. A mid-level navigation stack then generates collision-aware, dynamically feasible trajectories, while a centralized behavior manager coordinates high-level decision making, role selection, and kick execution based on the evolving game state. The seamless integration of these subsystems results in fast, precise, and tactically effective gameplay, enabling robust performance under the dynamic and adversarial conditions of real matches. This paper presents the design principles, system architecture, and experimental results that contributed to ARTEMIS's success as the 2024 Adult-Sized Humanoid Soccer champion.
CLAP: Clustering to Localize Across n Possibilities, A Simple, Robust Geometric Approach in the Presence of Symmetries
Sep 10, 2025Abstract:In this paper, we present our localization method called CLAP, Clustering to Localize Across $n$ Possibilities, which helped us win the RoboCup 2024 adult-sized autonomous humanoid soccer competition. Competition rules limited our sensor suite to stereo vision and an inertial sensor, similar to humans. In addition, our robot had to deal with varying lighting conditions, dynamic feature occlusions, noise from high-impact stepping, and mistaken features from bystanders and neighboring fields. Therefore, we needed an accurate, and most importantly robust localization algorithm that would be the foundation for our path-planning and game-strategy algorithms. CLAP achieves these requirements by clustering estimated states of our robot from pairs of field features to localize its global position and orientation. Correct state estimates naturally cluster together, while incorrect estimates spread apart, making CLAP resilient to noise and incorrect inputs. CLAP is paired with a particle filter and an extended Kalman filter to improve consistency and smoothness. Tests of CLAP with other landmark-based localization methods showed similar accuracy. However, tests with increased false positive feature detection showed that CLAP outperformed other methods in terms of robustness with very little divergence and velocity jumps. Our localization performed well in competition, allowing our robot to shoot faraway goals and narrowly defend our goal.
Feasibility Study of LIMMS, A Multi-Agent Modular Robotic Delivery System with Various Locomotion and Manipulation Modes
Aug 24, 2022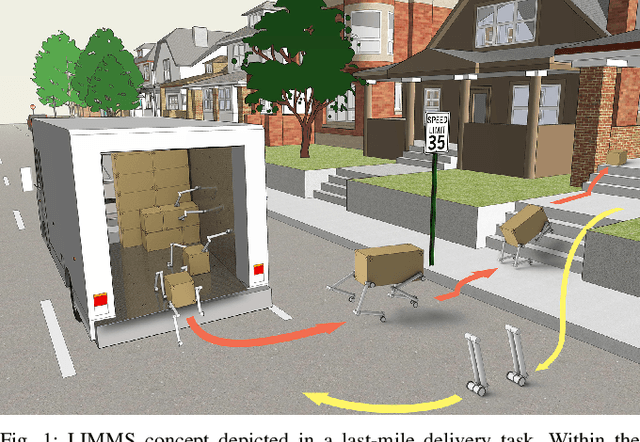

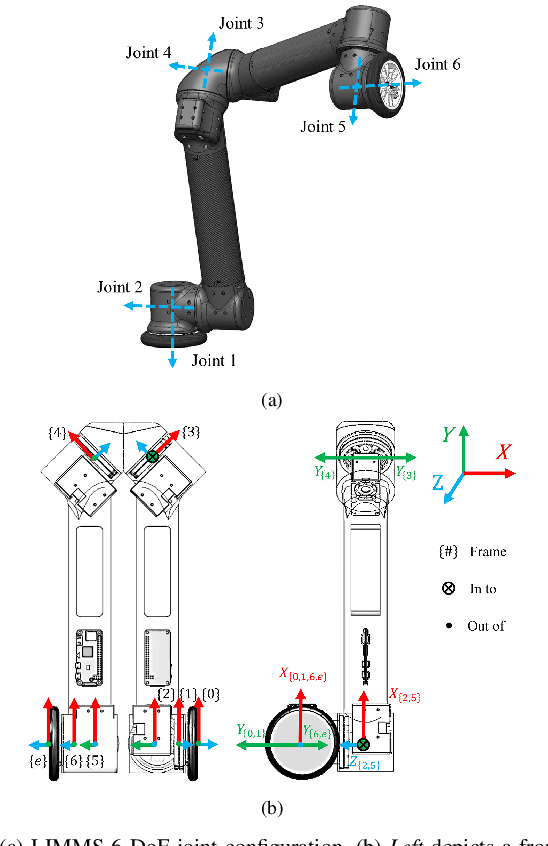
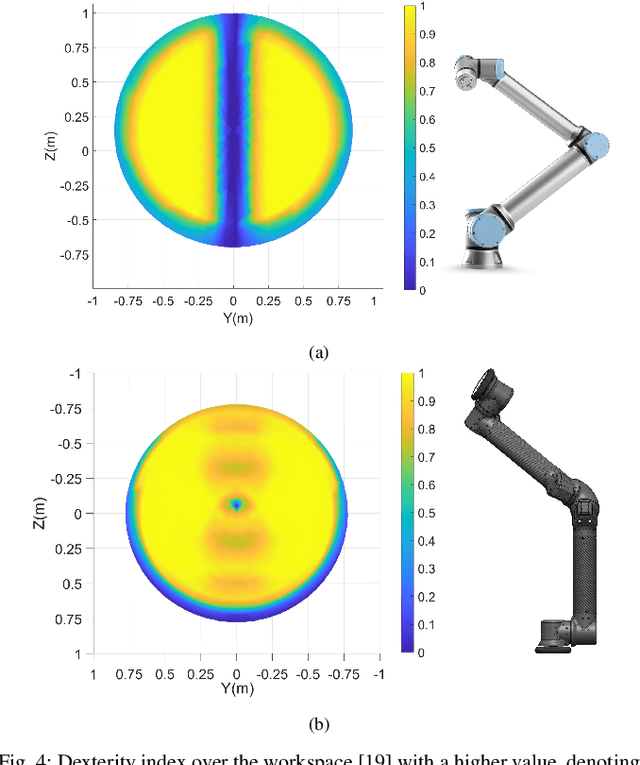
Abstract:The logistics of transporting a package from a storage facility to the consumer's front door usually employs highly specialized robots often times splitting sub-tasks up to different systems, e.g., manipulator arms to sort and wheeled vehicles to deliver. More recent endeavors attempt to have a unified approach with legged and humanoid robots. These solutions, however, occupy large amounts of space thus reducing the number of packages that can fit into a delivery vehicle. As a result, these bulky robotic systems often reduce the potential for scalability and task parallelization. In this paper, we introduce LIMMS (Latching Intelligent Modular Mobility System) to address both the manipulation and delivery portion of a typical last-mile delivery while maintaining a minimal spatial footprint. LIMMS is a symmetrically designed, 6 degree of freedom (DoF) appendage-like robot with wheels and latching mechanisms at both ends. By latching onto a surface and anchoring at one end, LIMMS can function as a traditional 6-DoF manipulator arm. On the other hand, multiple LIMMS can latch onto a single box and behave like a legged robotic system where the package is the body. During transit, LIMMS folds up compactly and takes up much less space compared to traditional robotic systems. A large group of LIMMS units can fit inside of a single delivery vehicle, opening the potential for new delivery optimization and hybrid planning methods never done before. In this paper, the feasibility of LIMMS is studied and presented using a hardware prototype as well as simulation results for a range of sub-tasks in a typical last-mile delivery.
Deep Reinforcement Learning with Linear Quadratic Regulator Regions
Feb 26, 2020

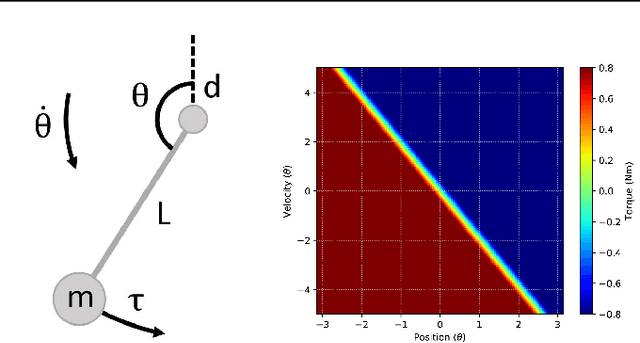
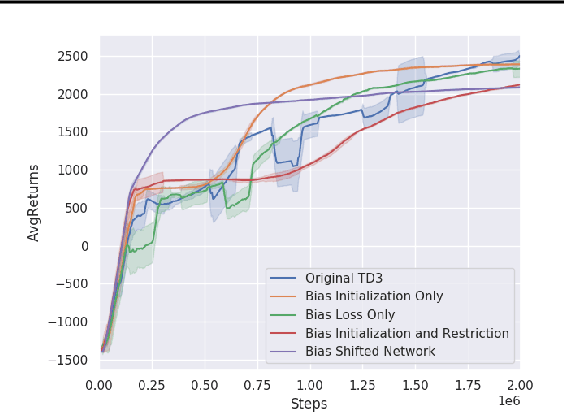
Abstract:Practitioners often rely on compute-intensive domain randomization to ensure reinforcement learning policies trained in simulation can robustly transfer to the real world. Due to unmodeled nonlinearities in the real system, however, even such simulated policies can still fail to perform stably enough to acquire experience in real environments. In this paper we propose a novel method that guarantees a stable region of attraction for the output of a policy trained in simulation, even for highly nonlinear systems. Our core technique is to use "bias-shifted" neural networks for constructing the controller and training the network in the simulator. The modified neural networks not only capture the nonlinearities of the system but also provably preserve linearity in a certain region of the state space and thus can be tuned to resemble a linear quadratic regulator that is known to be stable for the real system. We have tested our new method by transferring simulated policies for a swing-up inverted pendulum to real systems and demonstrated its efficacy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge