Over-parameterised Shallow Neural Networks with Asymmetrical Node Scaling: Global Convergence Guarantees and Feature Learning

We consider the optimisation of large and shallow neural networks via gradient flow, where the output of each hidden node is scaled by some positive parameter. We focus on the case where the node scalings are non-identical, differing from the classical Neural Tangent Kernel (NTK) parameterisation. We prove that, for large neural networks, with high probability, gradient flow converges to a global minimum AND can learn features, unlike in the NTK regime. We also provide experiments on synthetic and real-world datasets illustrating our theoretical results and showing the benefit of such scaling in terms of pruning and transfer learning.

Bayesian nonparametrics for Sparse Dynamic Networks

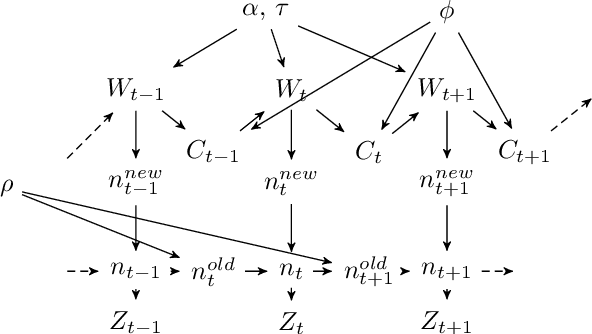
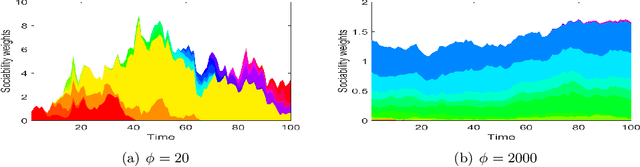
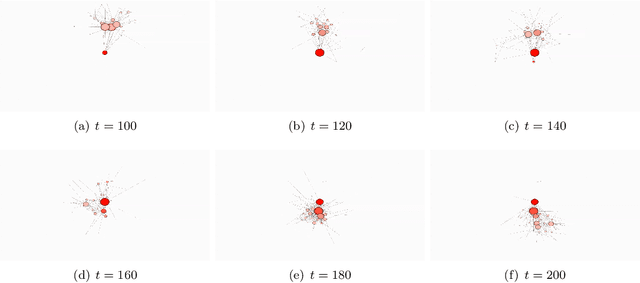
We propose a Bayesian nonparametric prior for time-varying networks. To each node of the network is associated a positive parameter, modeling the sociability of that node. Sociabilities are assumed to evolve over time, and are modeled via a dynamic point process model. The model is able to (a) capture smooth evolution of the interaction between nodes, allowing edges to appear/disappear over time (b) capture long term evolution of the sociabilities of the nodes (c) and yield sparse graphs, where the number of edges grows subquadratically with the number of nodes. The evolution of the sociabilities is described by a tractable time-varying gamma process. We provide some theoretical insights into the model and apply it to three real world datasets.

Bayesian nonparametric image segmentation using a generalized Swendsen-Wang algorithm

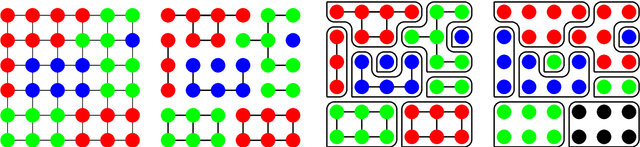
Unsupervised image segmentation aims at clustering the set of pixels of an image into spatially homogeneous regions. We introduce here a class of Bayesian nonparametric models to address this problem. These models are based on a combination of a Potts-like spatial smoothness component and a prior on partitions which is used to control both the number and size of clusters. This class of models is flexible enough to include the standard Potts model and the more recent Potts-Dirichlet Process model \cite{Orbanz2008}. More importantly, any prior on partitions can be introduced to control the global clustering structure so that it is possible to penalize small or large clusters if necessary. Bayesian computation is carried out using an original generalized Swendsen-Wang algorithm. Experiments demonstrate that our method is competitive in terms of RAND\ index compared to popular image segmentation methods, such as mean-shift, and recent alternative Bayesian nonparametric models.

Bayesian nonparametric models for ranked data

We develop a Bayesian nonparametric extension of the popular Plackett-Luce choice model that can handle an infinite number of choice items. Our framework is based on the theory of random atomic measures, with the prior specified by a gamma process. We derive a posterior characterization and a simple and effective Gibbs sampler for posterior simulation. We develop a time-varying extension of our model, and apply it to the New York Times lists of weekly bestselling books.

Efficient Bayesian Inference for Generalized Bradley-Terry Models

The Bradley-Terry model is a popular approach to describe probabilities of the possible outcomes when elements of a set are repeatedly compared with one another in pairs. It has found many applications including animal behaviour, chess ranking and multiclass classification. Numerous extensions of the basic model have also been proposed in the literature including models with ties, multiple comparisons, group comparisons and random graphs. From a computational point of view, Hunter (2004) has proposed efficient iterative MM (minorization-maximization) algorithms to perform maximum likelihood estimation for these generalized Bradley-Terry models whereas Bayesian inference is typically performed using MCMC (Markov chain Monte Carlo) algorithms based on tailored Metropolis-Hastings (M-H) proposals. We show here that these MM\ algorithms can be reinterpreted as special instances of Expectation-Maximization (EM) algorithms associated to suitable sets of latent variables and propose some original extensions. These latent variables allow us to derive simple Gibbs samplers for Bayesian inference. We demonstrate experimentally the efficiency of these algorithms on a variety of applications.