On the privacy-utility trade-off in differentially private hierarchical text classification

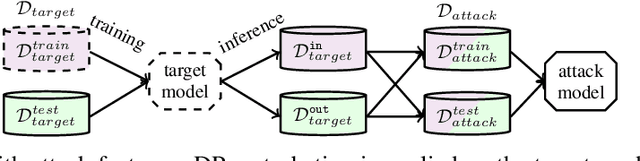
Hierarchical models for text classification can leak sensitive or confidential training data information to adversaries due to training data memorization. Using differential privacy during model training can mitigate leakage attacks against trained models by perturbing the training optimizer. However, for hierarchical text classification a multiplicity of model architectures is available and it is unclear whether some architectures yield a better trade-off between remaining model accuracy and model leakage under differentially private training perturbation than others. We use a white-box membership inference attack to assess the information leakage of three widely used neural network architectures for hierarchical text classification under differential privacy. We show that relatively weak differential privacy guarantees already suffice to completely mitigate the membership inference attack, thus resulting only in a moderate decrease in utility. More specifically, for large datasets with long texts we observed transformer-based models to achieve an overall favorable privacy-utility trade-off, while for smaller datasets with shorter texts CNNs are preferable.

Pain-Free Random Differential Privacy with Sensitivity Sampling

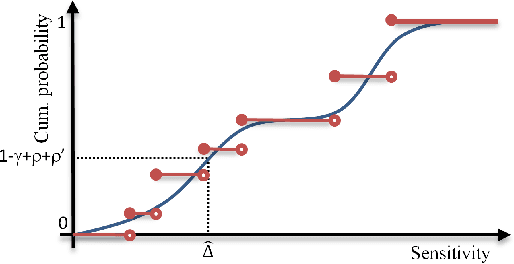
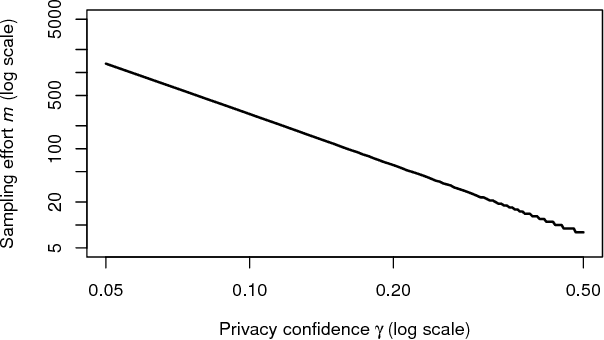
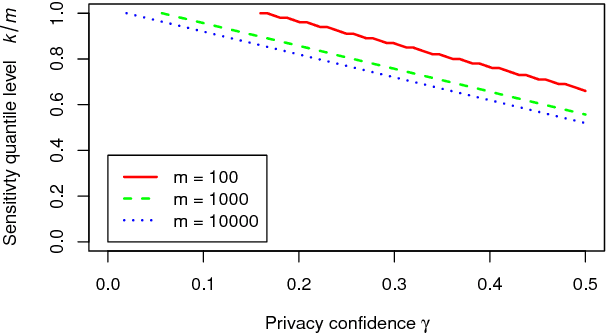
Popular approaches to differential privacy, such as the Laplace and exponential mechanisms, calibrate randomised smoothing through global sensitivity of the target non-private function. Bounding such sensitivity is often a prohibitively complex analytic calculation. As an alternative, we propose a straightforward sampler for estimating sensitivity of non-private mechanisms. Since our sensitivity estimates hold with high probability, any mechanism that would be $(\epsilon,\delta)$-differentially private under bounded global sensitivity automatically achieves $(\epsilon,\delta,\gamma)$-random differential privacy (Hall et al., 2012), without any target-specific calculations required. We demonstrate on worked example learners how our usable approach adopts a naturally-relaxed privacy guarantee, while achieving more accurate releases even for non-private functions that are black-box computer programs.