Pain-Free Random Differential Privacy with Sensitivity Sampling
Paper and Code
Jun 08, 2017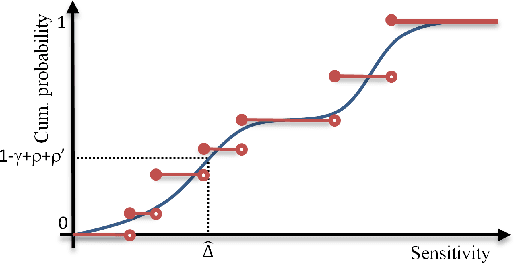

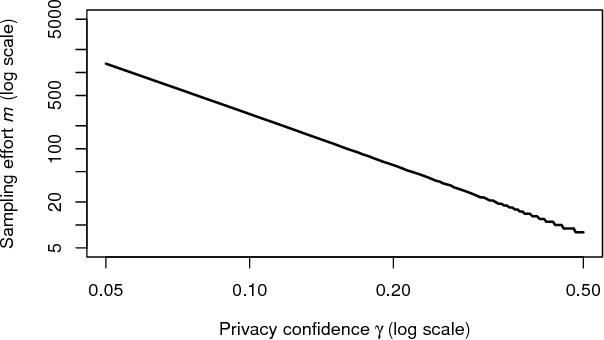
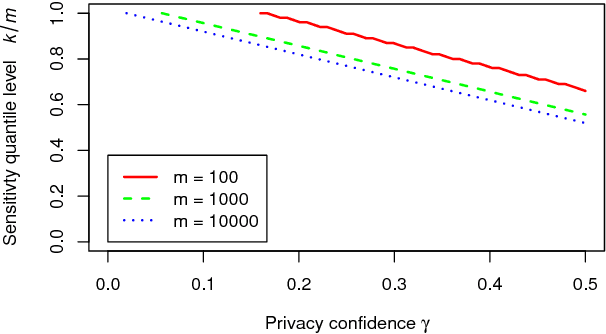
Popular approaches to differential privacy, such as the Laplace and exponential mechanisms, calibrate randomised smoothing through global sensitivity of the target non-private function. Bounding such sensitivity is often a prohibitively complex analytic calculation. As an alternative, we propose a straightforward sampler for estimating sensitivity of non-private mechanisms. Since our sensitivity estimates hold with high probability, any mechanism that would be $(\epsilon,\delta)$-differentially private under bounded global sensitivity automatically achieves $(\epsilon,\delta,\gamma)$-random differential privacy (Hall et al., 2012), without any target-specific calculations required. We demonstrate on worked example learners how our usable approach adopts a naturally-relaxed privacy guarantee, while achieving more accurate releases even for non-private functions that are black-box computer programs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge