Fading memory and the convolution theorem

Several topological and analytical notions of continuity and fading memory for causal and time-invariant filters are introduced, and the relations between them are analysed. A significant generalization of the convolution theorem that establishes the equivalence between the fading memory property and the availability of convolution representations of linear filters is proved. This result extends a previous such characterization to a complete array of weighted norms in the definition of the fading memory property. Additionally, the main theorem shows that the availability of convolution representations can be characterized, at least when the codomain is finite-dimensional, not only by the fading memory property but also by the reunion of two purely topological notions that are called minimal continuity and minimal fading memory property. Finally, when the input space and the codomain of a linear functional are Hilbert spaces, it is shown that minimal continuity and the minimal fading memory property guarantee the existence of interesting embeddings of the associated reproducing kernel Hilbert spaces and approximation results of solutions of kernel regressions in the presence of finite data sets.

State-Space Systems as Dynamic Generative Models

A probabilistic framework to study the dependence structure induced by deterministic discrete-time state-space systems between input and output processes is introduced. General sufficient conditions are formulated under which output processes exist and are unique once an input process has been fixed, a property that in the deterministic state-space literature is known as the echo state property. When those conditions are satisfied, the given state-space system becomes a generative model for probabilistic dependences between two sequence spaces. Moreover, those conditions guarantee that the output depends continuously on the input when using the Wasserstein metric. The output processes whose existence is proved are shown to be causal in a specific sense and to generalize those studied in purely deterministic situations. The results in this paper constitute a significant stochastic generalization of sufficient conditions for the deterministic echo state property to hold, in the sense that the stochastic echo state property can be satisfied under contractivity conditions that are strictly weaker than those in deterministic situations. This means that state-space systems can induce a purely probabilistic dependence structure between input and output sequence spaces even when there is no functional relation between those two spaces.

Gradient descent provably escapes saddle points in the training of shallow ReLU networks

Dynamical systems theory has recently been applied in optimization to prove that gradient descent algorithms avoid so-called strict saddle points of the loss function. However, in many modern machine learning applications, the required regularity conditions are not satisfied. In particular, this is the case for rectified linear unit (ReLU) networks. In this paper, we prove a variant of the relevant dynamical systems result, a center-stable manifold theorem, in which we relax some of the regularity requirements. Then, we verify that shallow ReLU networks fit into the new framework. Building on a classification of critical points of the square integral loss of shallow ReLU networks measured against an affine target function, we deduce that gradient descent avoids most saddle points. We proceed to prove convergence to global minima if the initialization is sufficiently good, which is expressed by an explicit threshold on the limiting loss.

Landscape analysis for shallow ReLU neural networks: complete classification of critical points for affine target functions

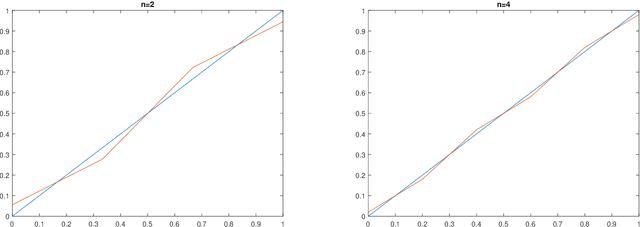
In this paper, we analyze the landscape of the true loss of a ReLU neural network with one hidden layer. We provide a complete classification of the critical points in the case where the target function is affine. In particular, we prove that local minima and saddle points have to be of a special form and show that there are no local maxima. Our approach is of a combinatorial nature and builds on a careful analysis of the different types of hidden neurons that can occur in a ReLU neural network.

A proof of convergence for gradient descent in the training of artificial neural networks for constant target functions

Gradient descent optimization algorithms are the standard ingredients that are used to train artificial neural networks (ANNs). Even though a huge number of numerical simulations indicate that gradient descent optimization methods do indeed convergence in the training of ANNs, until today there is no rigorous theoretical analysis which proves (or disproves) this conjecture. In particular, even in the case of the most basic variant of gradient descent optimization algorithms, the plain vanilla gradient descent method, it remains an open problem to prove or disprove the conjecture that gradient descent converges in the training of ANNs. In this article we solve this problem in the special situation where the target function under consideration is a constant function. More specifically, in the case of constant target functions we prove in the training of rectified fully-connected feedforward ANNs with one-hidden layer that the risk function of the gradient descent method does indeed converge to zero. Our mathematical analysis strongly exploits the property that the rectifier function is the activation function used in the considered ANNs. A key contribution of this work is to explicitly specify a Lyapunov function for the gradient flow system of the ANN parameters. This Lyapunov function is the central tool in our convergence proof of the gradient descent method.

Non-convergence of stochastic gradient descent in the training of deep neural networks

Deep neural networks have successfully been trained in various application areas with stochastic gradient descent. However, there exists no rigorous mathematical explanation why this works so well. The training of neural networks with stochastic gradient descent has four different discretization parameters: (i) the network architecture; (ii) the size of the training data; (iii) the number of gradient steps; and (iv) the number of randomly initialized gradient trajectories. While it can be shown that the approximation error converges to zero if all four parameters are sent to infinity in the right order, we demonstrate in this paper that stochastic gradient descent fails to converge for rectified linear unit networks if their depth is much larger than their width and the number of random initializations does not increase to infinity fast enough.