Lightweight Online Learning for Sets of Related Problems in Automated Reasoning

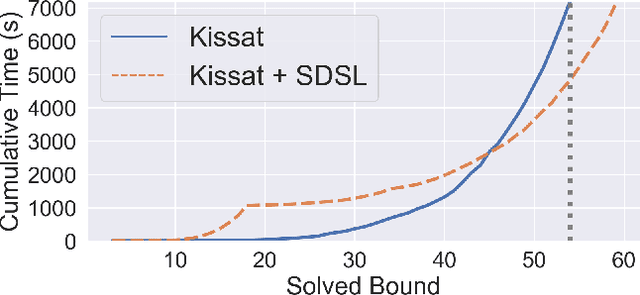
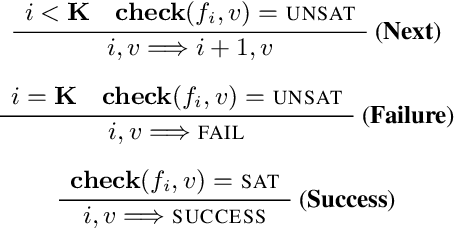
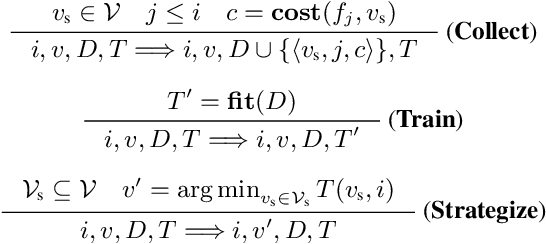
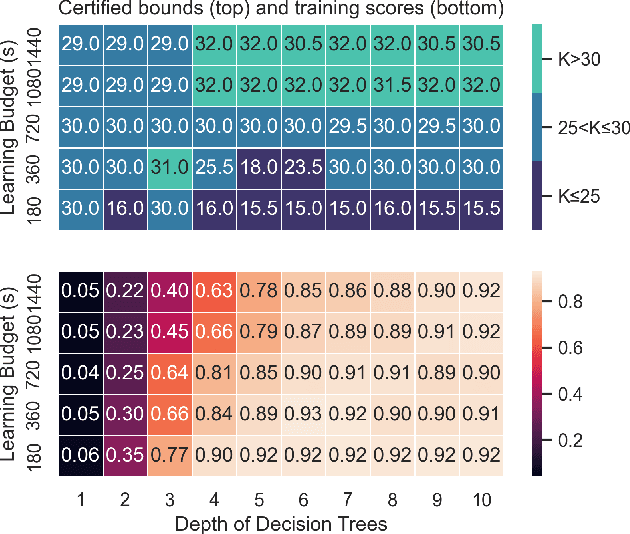
We present Self-Driven Strategy Learning ($\textit{sdsl}$), a lightweight online learning methodology for automated reasoning tasks that involve solving a set of related problems. $\textit{sdsl}$ does not require offline training, but instead automatically constructs a dataset while solving earlier problems. It fits a machine learning model to this data which is then used to adjust the solving strategy for later problems. We formally define the approach as a set of abstract transition rules. We describe a concrete instance of the sdsl calculus which uses conditional sampling for generating data and random forests as the underlying machine learning model. We implement the approach on top of the Kissat solver and show that the combination of Kissat+$\textit{sdsl}$ certifies larger bounds and finds more counter-examples than other state-of-the-art bounded model checking approaches on benchmarks obtained from the latest Hardware Model Checking Competition.

HordeQBF: A Modular and Massively Parallel QBF Solver

The recently developed massively parallel satisfiability (SAT) solver HordeSAT was designed in a modular way to allow the integration of any sequential CDCL-based SAT solver in its core. We integrated the QCDCL-based quantified Boolean formula (QBF) solver DepQBF in HordeSAT to obtain a massively parallel QBF solver---HordeQBF. In this paper we describe the details of this integration and report on results of the experimental evaluation of HordeQBF's performance. HordeQBF achieves superlinear average and median speedup on the hard application instances of the 2014 QBF Gallery.

Conformant Planning as a Case Study of Incremental QBF Solving

We consider planning with uncertainty in the initial state as a case study of incremental quantified Boolean formula (QBF) solving. We report on experiments with a workflow to incrementally encode a planning instance into a sequence of QBFs. To solve this sequence of incrementally constructed QBFs, we use our general-purpose incremental QBF solver DepQBF. Since the generated QBFs have many clauses and variables in common, our approach avoids redundancy both in the encoding phase and in the solving phase. Experimental results show that incremental QBF solving outperforms non-incremental QBF solving. Our results are the first empirical study of incremental QBF solving in the context of planning and motivate its use in other application domains.