Inverse Kinematics for Serial Kinematic Chains via Sum of Squares Optimization

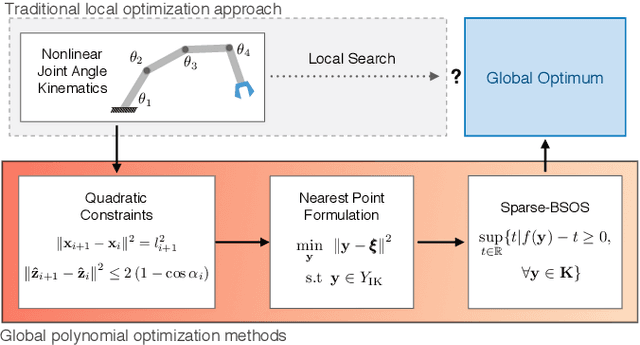
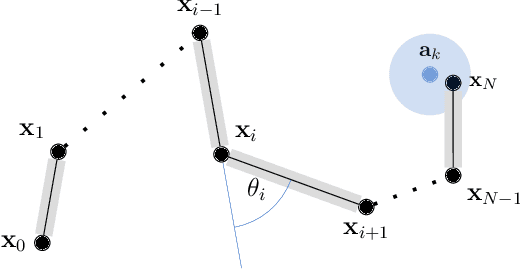
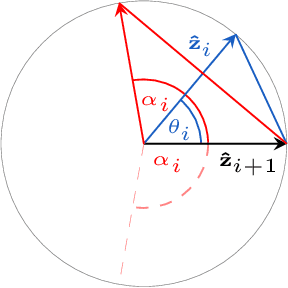
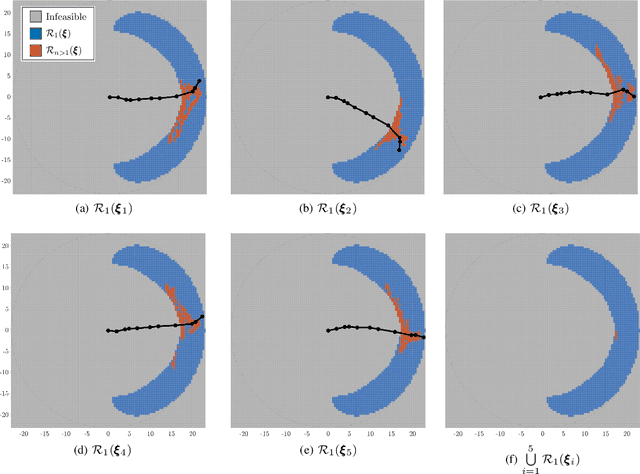
Inverse kinematics is a fundamental problem for articulated robots: fast and accurate algorithms are needed for translating task-related workspace constraints and goals into feasible joint configurations. In general, inverse kinematics for serial kinematic chains is a difficult nonlinear problem, for which closed form solutions cannot be easily obtained. Therefore, computationally efficient numerical methods that can be adapted to a general class of manipulators are of great importance. % to motion planning and workspace generation tasks. In this paper, we use convex optimization techniques to solve the inverse kinematics problem with joint limit constraints for highly redundant serial kinematic chains with spherical joints in two and three dimensions. This is accomplished through a novel formulation of inverse kinematics as a nearest point problem, and with a fast sum of squares solver that exploits the sparsity of kinematic constraints for serial manipulators. Our method has the advantages of post-hoc certification of global optimality and a runtime that scales polynomialy with the number of degrees of freedom. Additionally, we prove that our convex relaxation leads to a globally optimal solution when certain conditions are met, and demonstrate empirically that these conditions are common and represent many practical instances. Finally, we provide an open source implementation of our algorithm.

Sparse Bounded Degree Sum of Squares Optimization for Certifiably Globally Optimal Rotation Averaging

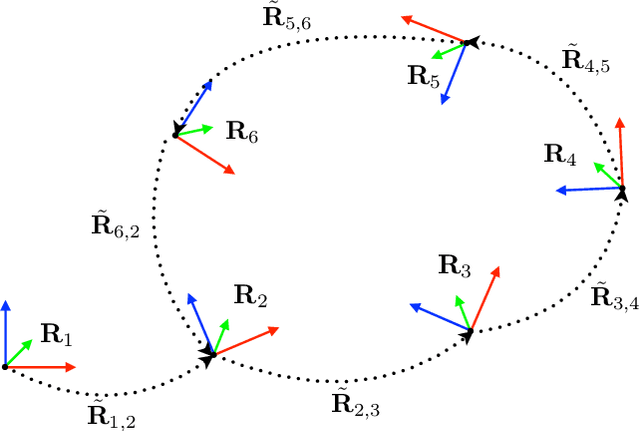
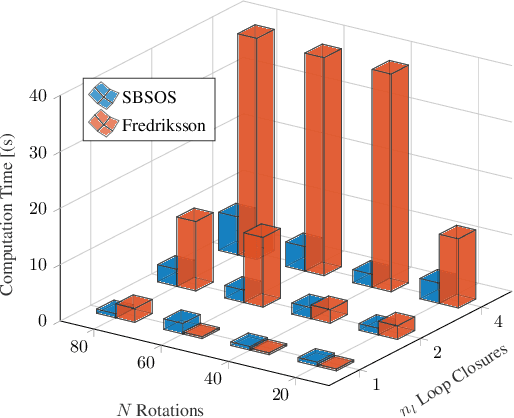
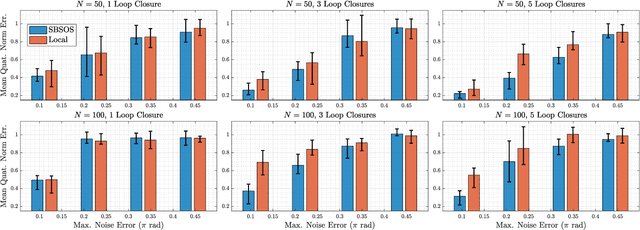
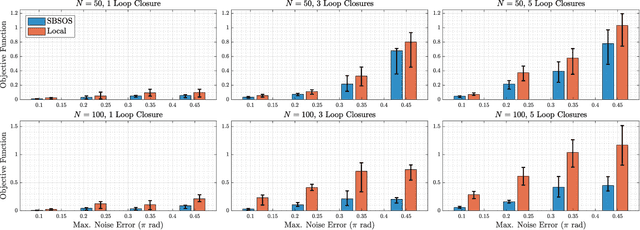
Estimating unknown rotations from noisy measurements is an important step in SfM and other 3D vision tasks. Typically, local optimization methods susceptible to returning suboptimal local minima are used to solve the rotation averaging problem. A new wave of approaches that leverage convex relaxations have provided the first formal guarantees of global optimality for state estimation techniques involving SO(3). However, most of these guarantees are only applicable when the measurement error introduced by noise is within a certain bound that depends on the problem instance's structure. In this paper, we cast rotation averaging as a polynomial optimization problem over unit quaternions to produce the first rotation averaging method that is formally guaranteed to provide a certifiably globally optimal solution for \textit{any} problem instance. This is achieved by formulating and solving a sparse convex sum of squares (SOS) relaxation of the problem. We provide an open source implementation of our algorithm and experiments, demonstrating the benefits of our globally optimal approach.

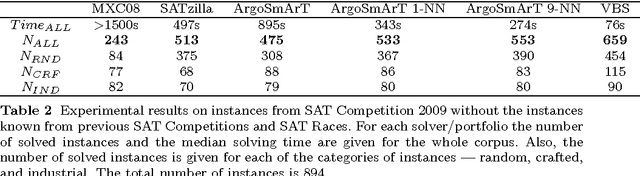
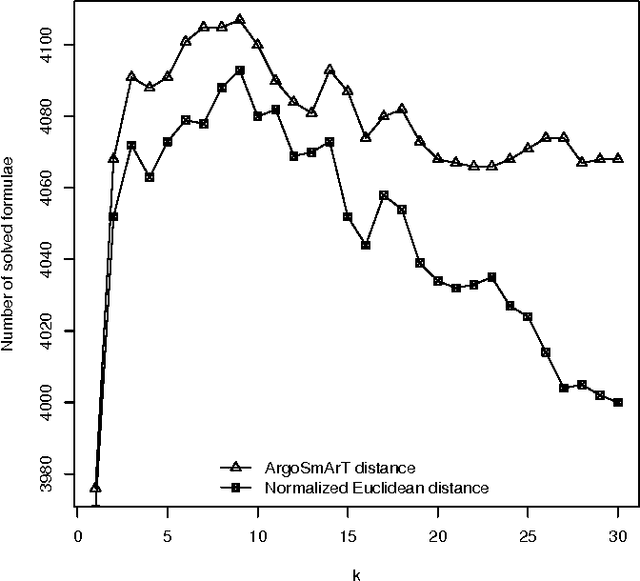
Simple Algorithm Portfolio for SAT

The importance of algorithm portfolio techniques for SAT has long been noted, and a number of very successful systems have been devised, including the most successful one --- SATzilla. However, all these systems are quite complex (to understand, reimplement, or modify). In this paper we propose a new algorithm portfolio for SAT that is extremely simple, but in the same time so efficient that it outperforms SATzilla. For a new SAT instance to be solved, our portfolio finds its k-nearest neighbors from the training set and invokes a solver that performs the best at those instances. The main distinguishing feature of our algorithm portfolio is the locality of the selection procedure --- the selection of a SAT solver is based only on few instances similar to the input one.