Predrag Janicic
University of Belgrade
URSA: A System for Uniform Reduction to SAT
Sep 28, 2012



Abstract:There are a huge number of problems, from various areas, being solved by reducing them to SAT. However, for many applications, translation into SAT is performed by specialized, problem-specific tools. In this paper we describe a new system for uniform solving of a wide class of problems by reducing them to SAT. The system uses a new specification language URSA that combines imperative and declarative programming paradigms. The reduction to SAT is defined precisely by the semantics of the specification language. The domain of the approach is wide (e.g., many NP-complete problems can be simply specified and then solved by the system) and there are problems easily solvable by the proposed system, while they can be hardly solved by using other programming languages or constraint programming systems. So, the system can be seen not only as a tool for solving problems by reducing them to SAT, but also as a general-purpose constraint solving system (for finite domains). In this paper, we also describe an open-source implementation of the described approach. The performed experiments suggest that the system is competitive to state-of-the-art related modelling systems.
* 39 pages, uses tikz.sty
Towards Understanding Triangle Construction Problems
Jul 18, 2012
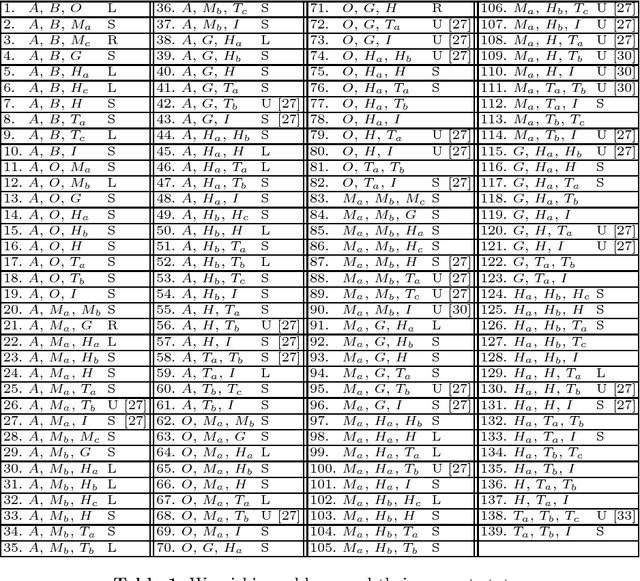
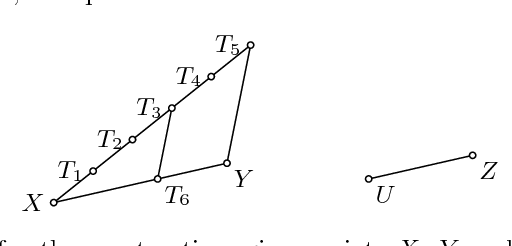
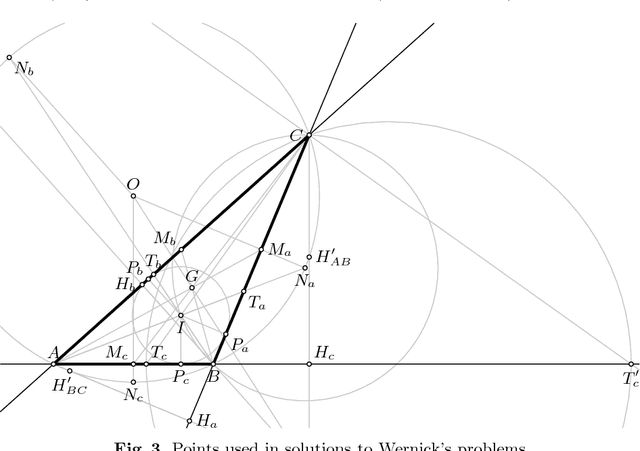
Abstract:Straightedge and compass construction problems are one of the oldest and most challenging problems in elementary mathematics. The central challenge, for a human or for a computer program, in solving construction problems is a huge search space. In this paper we analyze one family of triangle construction problems, aiming at detecting a small core of the underlying geometry knowledge. The analysis leads to a small set of needed definitions, lemmas and primitive construction steps, and consequently, to a simple algorithm for automated solving of problems from this family. The same approach can be applied to other families of construction problems.
Simple Algorithm Portfolio for SAT
Dec 13, 2011
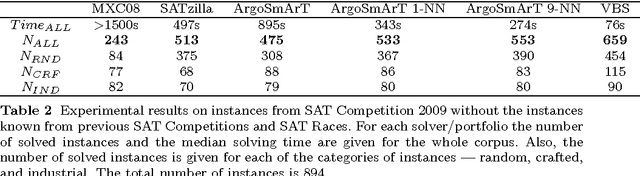
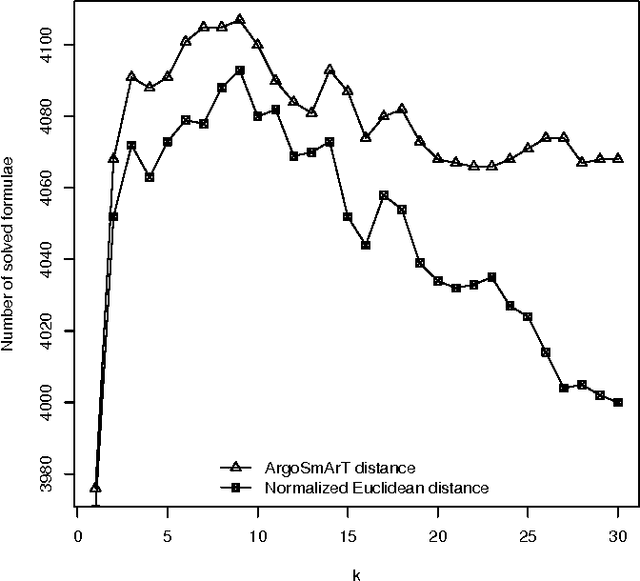
Abstract:The importance of algorithm portfolio techniques for SAT has long been noted, and a number of very successful systems have been devised, including the most successful one --- SATzilla. However, all these systems are quite complex (to understand, reimplement, or modify). In this paper we propose a new algorithm portfolio for SAT that is extremely simple, but in the same time so efficient that it outperforms SATzilla. For a new SAT instance to be solved, our portfolio finds its k-nearest neighbors from the training set and invokes a solver that performs the best at those instances. The main distinguishing feature of our algorithm portfolio is the locality of the selection procedure --- the selection of a SAT solver is based only on few instances similar to the input one.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge