Towards Understanding Triangle Construction Problems
Paper and Code
Jul 18, 2012
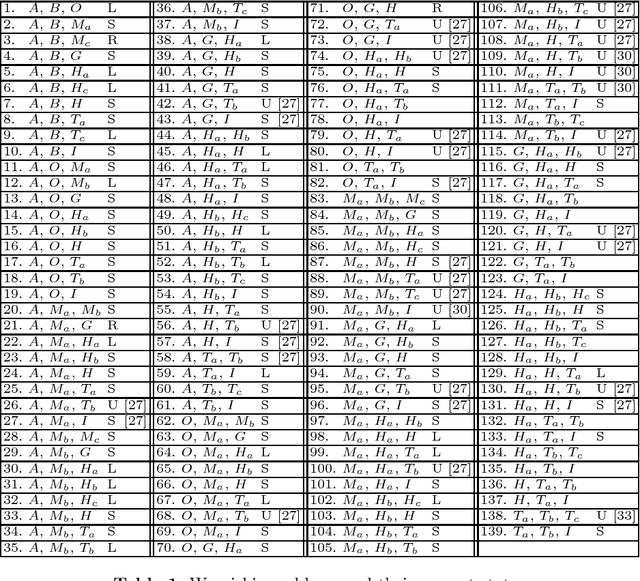
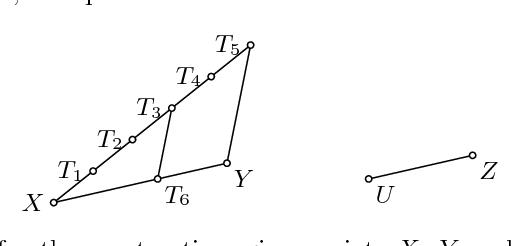
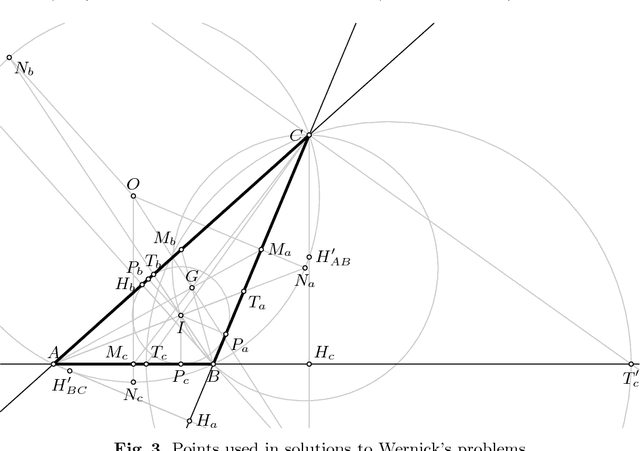
Straightedge and compass construction problems are one of the oldest and most challenging problems in elementary mathematics. The central challenge, for a human or for a computer program, in solving construction problems is a huge search space. In this paper we analyze one family of triangle construction problems, aiming at detecting a small core of the underlying geometry knowledge. The analysis leads to a small set of needed definitions, lemmas and primitive construction steps, and consequently, to a simple algorithm for automated solving of problems from this family. The same approach can be applied to other families of construction problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge