Simple Algorithm Portfolio for SAT
Paper and Code
Dec 13, 2011
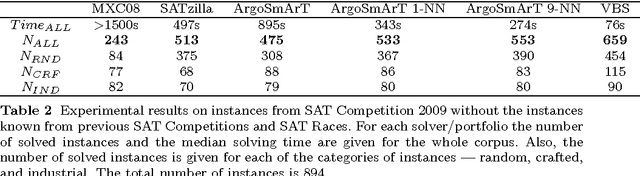
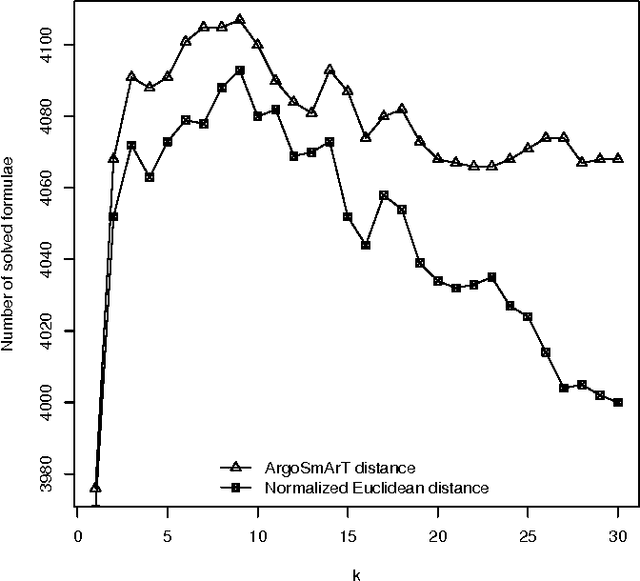
The importance of algorithm portfolio techniques for SAT has long been noted, and a number of very successful systems have been devised, including the most successful one --- SATzilla. However, all these systems are quite complex (to understand, reimplement, or modify). In this paper we propose a new algorithm portfolio for SAT that is extremely simple, but in the same time so efficient that it outperforms SATzilla. For a new SAT instance to be solved, our portfolio finds its k-nearest neighbors from the training set and invokes a solver that performs the best at those instances. The main distinguishing feature of our algorithm portfolio is the locality of the selection procedure --- the selection of a SAT solver is based only on few instances similar to the input one.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge