Riemannian Optimization for Distance Geometric Inverse Kinematics

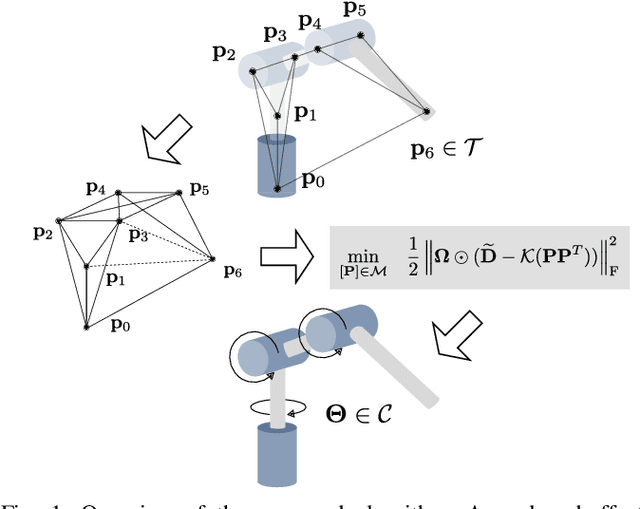
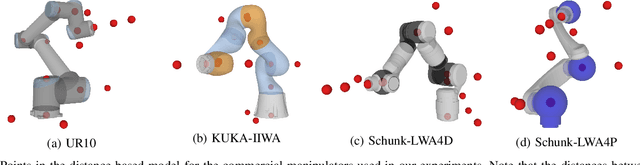
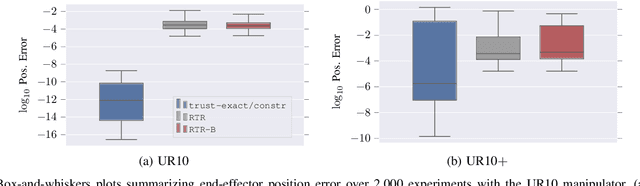
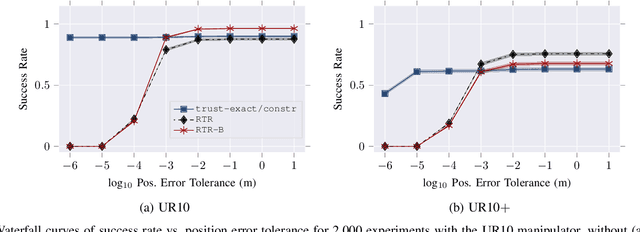
Solving the inverse kinematics problem is a fundamental challenge in motion planning, control, and calibration for articulated robots. Kinematic models for these robots are typically parameterized by joint angles, generating a complicated mapping between a robot's configuration and end-effector pose. Alternatively, the kinematic model and task constraints can be represented using invariant distances between points attached to the robot. In this paper, we formalize the equivalence of distance-based inverse kinematics and the distance geometry problem for a large class of articulated robots and task constraints. Unlike previous approaches, we use the connection between distance geometry and low-rank matrix completion to find inverse kinematics solutions by completing a partial Euclidean distance matrix through local optimization. Furthermore, we parameterize the space of Euclidean distance matrices with the Riemannian manifold of fixed-rank Gram matrices, allowing us to leverage a variety of mature Riemannian optimization methods. Finally, we show that bound smoothing can be used to generate informed initializations without significant computational overhead, improving convergence. We demonstrate that our novel inverse kinematics solver achieves higher success rates than traditional techniques, and significantly outperforms them on problems that involve many workspace constraints.

Certifiably Optimal Monocular Hand-Eye Calibration

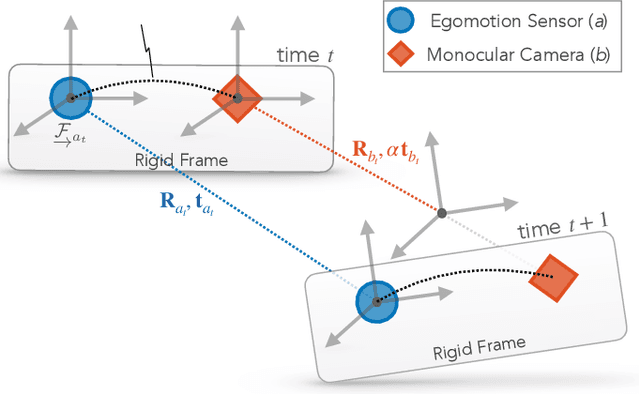
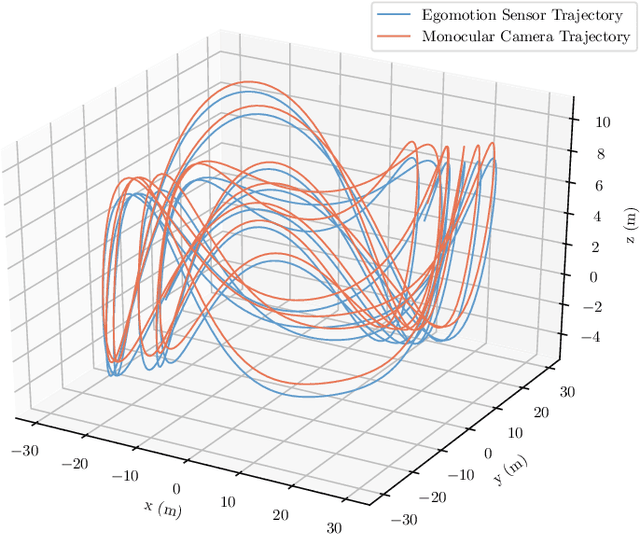
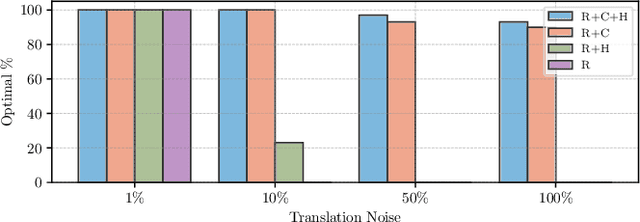
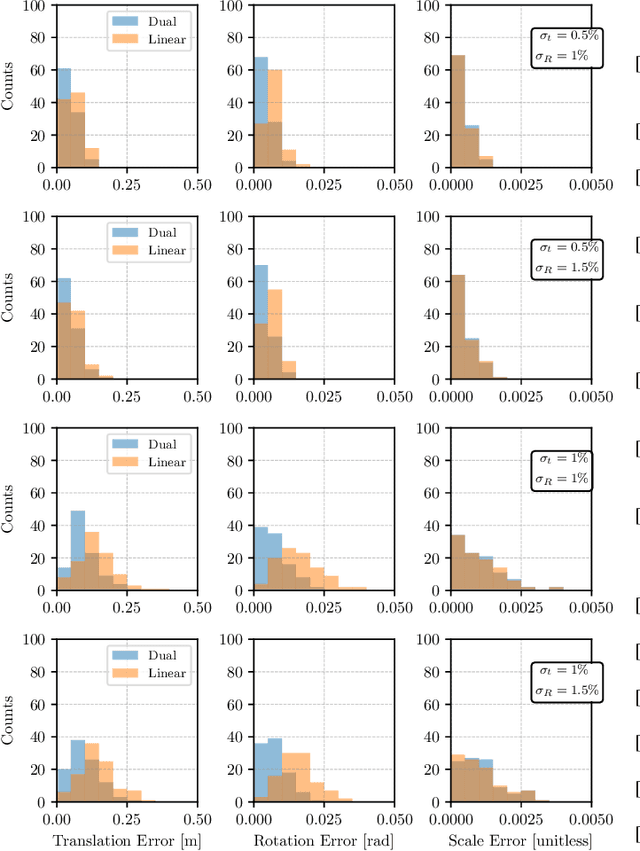
Correct fusion of data from two sensors is not possible without an accurate estimate of their relative pose, which can be determined through the process of extrinsic calibration. When two or more sensors are capable of producing their own egomotion estimates (i.e., measurements of their trajectories through an environment), the 'hand-eye' formulation of extrinsic calibration can be employed. In this paper, we extend our recent work on a convex optimization approach for hand-eye calibration to the case where one of the sensors cannot observe the scale of its translational motion (e.g., a monocular camera observing an unmapped environment). We prove that our technique is able to provide a certifiably globally optimal solution to both the known- and unknown-scale variants of hand-eye calibration, provided that the measurement noise is bounded. Herein, we focus on the theoretical aspects of the problem, show the tightness and stability of our solution, and demonstrate the optimality and speed of our algorithm through experiments with synthetic data.

Inverse Kinematics for Serial Kinematic Chains via Sum of Squares Optimization

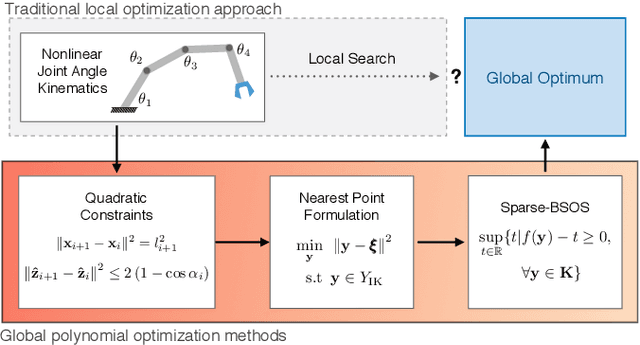
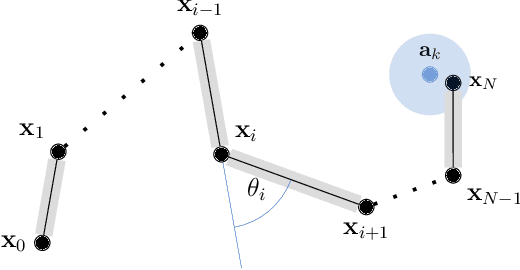
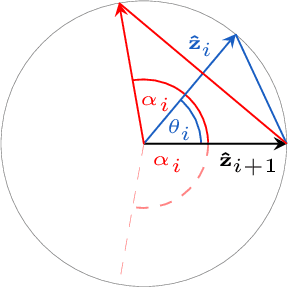
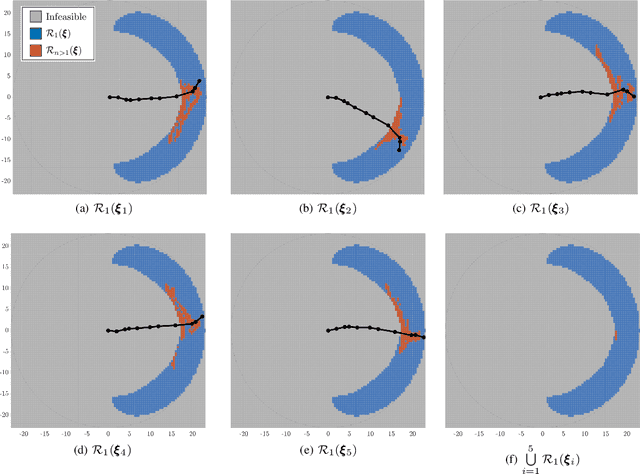
Inverse kinematics is a fundamental problem for articulated robots: fast and accurate algorithms are needed for translating task-related workspace constraints and goals into feasible joint configurations. In general, inverse kinematics for serial kinematic chains is a difficult nonlinear problem, for which closed form solutions cannot be easily obtained. Therefore, computationally efficient numerical methods that can be adapted to a general class of manipulators are of great importance. % to motion planning and workspace generation tasks. In this paper, we use convex optimization techniques to solve the inverse kinematics problem with joint limit constraints for highly redundant serial kinematic chains with spherical joints in two and three dimensions. This is accomplished through a novel formulation of inverse kinematics as a nearest point problem, and with a fast sum of squares solver that exploits the sparsity of kinematic constraints for serial manipulators. Our method has the advantages of post-hoc certification of global optimality and a runtime that scales polynomialy with the number of degrees of freedom. Additionally, we prove that our convex relaxation leads to a globally optimal solution when certain conditions are met, and demonstrate empirically that these conditions are common and represent many practical instances. Finally, we provide an open source implementation of our algorithm.