Towards Practical Adam: Non-Convexity, Convergence Theory, and Mini-Batch Acceleration

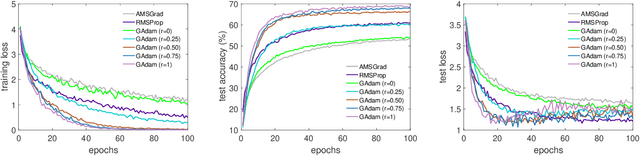
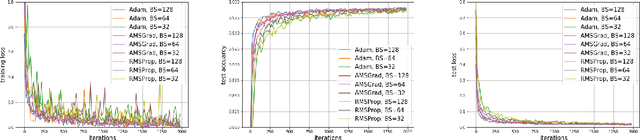
Adam is one of the most influential adaptive stochastic algorithms for training deep neural networks, which has been pointed out to be divergent even in the simple convex setting via a few simple counterexamples. Many attempts, such as decreasing an adaptive learning rate, adopting a big batch size, incorporating a temporal decorrelation technique, seeking an analogous surrogate, \textit{etc.}, have been tried to promote Adam-type algorithms to converge. In contrast with existing approaches, we introduce an alternative easy-to-check sufficient condition, which merely depends on the parameters of the base learning rate and combinations of historical second-order moments, to guarantee the global convergence of generic Adam for solving large-scale non-convex stochastic optimization. This observation coupled with this sufficient condition gives much deeper interpretations on the divergence of Adam. On the other hand, in practice, mini-Adam and distributed-Adam are widely used without theoretical guarantee, we further give an analysis on how will the batch size or the number of nodes in the distributed system will affect the convergence of Adam, which theoretically shows that mini-batch and distributed Adam can be linearly accelerated by using a larger mini-batch size or more number of nodes. At last, we apply the generic Adam and mini-batch Adam with a sufficient condition for solving the counterexample and training several different neural networks on various real-world datasets. Experimental results are exactly in accord with our theoretical analysis.

A Sufficient Condition for Convergences of Adam and RMSProp

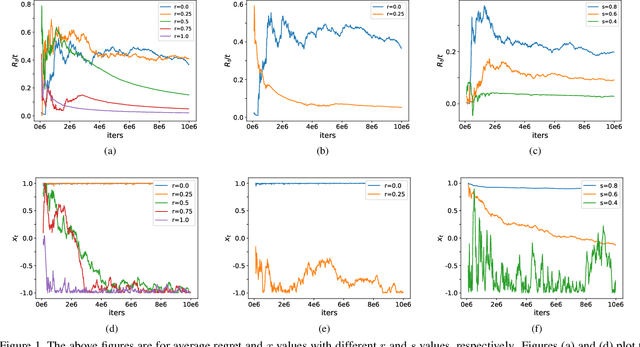
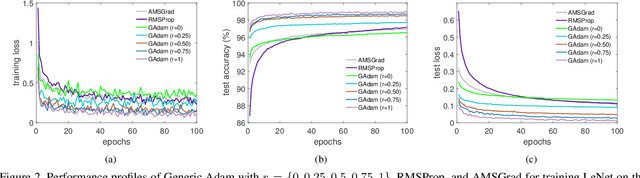
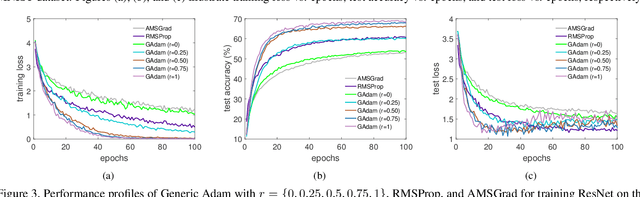
Adam and RMSProp, as two of the most influential adaptive stochastic algorithms for training deep neural networks, have been pointed out to be divergent even in the convex setting via a few simple counterexamples. Many attempts, such as decreasing an adaptive learning rate, adopting a big batch size, incorporating a temporal decorrelation technique, seeking an analogous surrogate, \textit{etc.}, have been tried to promote Adam/RMSProp-type algorithms to converge. In contrast with existing approaches, we introduce an alternative easy-to-check sufficient condition, which merely depends on the parameters of the base learning rate and combinations of historical second-order moments, to guarantee the global convergence of generic Adam/RMSProp for solving large-scale non-convex stochastic optimization. Moreover, we show that the convergences of several variants of Adam, such as AdamNC, AdaEMA, \textit{etc.}, can be directly implied via the proposed sufficient condition in the non-convex setting. In addition, we illustrate that Adam is essentially a specifically weighted AdaGrad with exponential moving average momentum, which provides a novel perspective for understanding Adam and RMSProp. This observation together with this sufficient condition gives much deeper interpretations on their divergences. At last, we validate the sufficient condition by applying Adam and RMSProp to tackle the counterexamples and train deep neural networks. Numerical results are exactly in accord with the analysis in theory.

On the Convergence of Weighted AdaGrad with Momentum for Training Deep Neural Networks

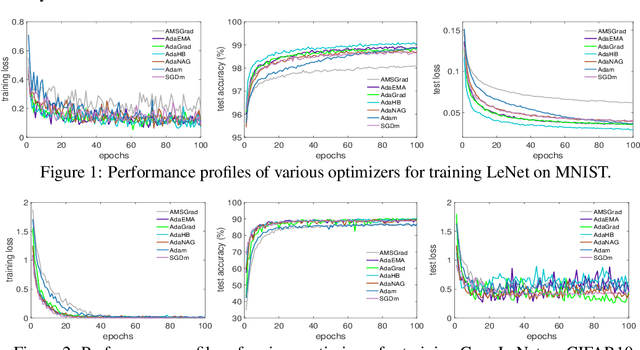
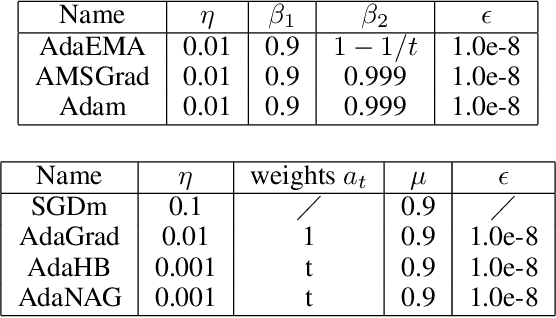
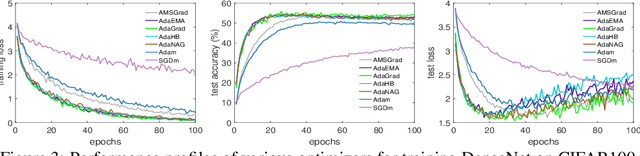
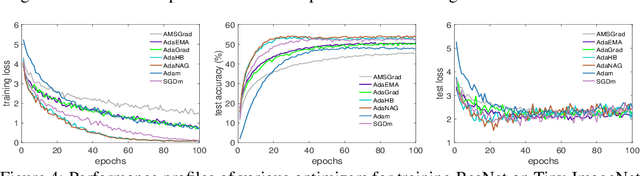
Adaptive stochastic gradient descent methods, such as AdaGrad, RMSProp, Adam, AMSGrad, etc., have been demonstrated efficacious in solving non-convex stochastic optimization, such as training deep neural networks. However, their convergence rates have not been touched under the non-convex stochastic circumstance except recent breakthrough results on AdaGrad, perturbed AdaGrad and AMSGrad. In this paper, we propose two new adaptive stochastic gradient methods called AdaHB and AdaNAG which integrate a novel weighted coordinate-wise AdaGrad with heavy ball momentum and Nesterov accelerated gradient momentum, respectively. The $\mathcal{O}(\frac{\log{T}}{\sqrt{T}})$ non-asymptotic convergence rates of AdaHB and AdaNAG in non-convex stochastic setting are also jointly established by leveraging a newly developed unified formulation of these two momentum mechanisms. Moreover, comparisons have been made between AdaHB, AdaNAG, Adam and RMSProp, which, to a certain extent, explains the reasons why Adam and RMSProp are divergent. In particular, when momentum term vanishes we obtain convergence rate of coordinate-wise AdaGrad in non-convex stochastic setting as a byproduct.