A Sufficient Condition for Convergences of Adam and RMSProp

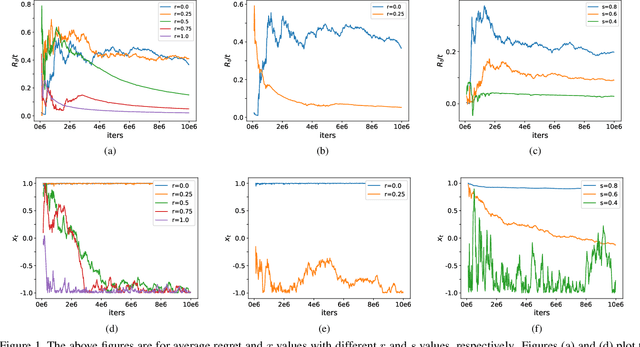
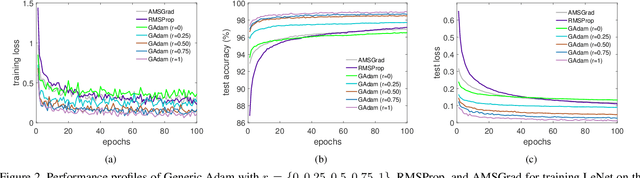
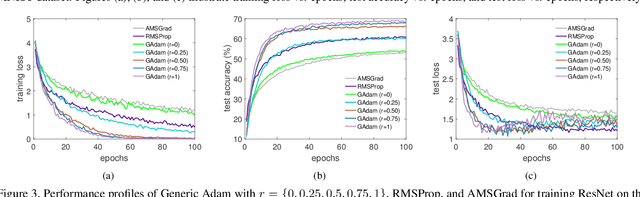
Adam and RMSProp, as two of the most influential adaptive stochastic algorithms for training deep neural networks, have been pointed out to be divergent even in the convex setting via a few simple counterexamples. Many attempts, such as decreasing an adaptive learning rate, adopting a big batch size, incorporating a temporal decorrelation technique, seeking an analogous surrogate, \textit{etc.}, have been tried to promote Adam/RMSProp-type algorithms to converge. In contrast with existing approaches, we introduce an alternative easy-to-check sufficient condition, which merely depends on the parameters of the base learning rate and combinations of historical second-order moments, to guarantee the global convergence of generic Adam/RMSProp for solving large-scale non-convex stochastic optimization. Moreover, we show that the convergences of several variants of Adam, such as AdamNC, AdaEMA, \textit{etc.}, can be directly implied via the proposed sufficient condition in the non-convex setting. In addition, we illustrate that Adam is essentially a specifically weighted AdaGrad with exponential moving average momentum, which provides a novel perspective for understanding Adam and RMSProp. This observation together with this sufficient condition gives much deeper interpretations on their divergences. At last, we validate the sufficient condition by applying Adam and RMSProp to tackle the counterexamples and train deep neural networks. Numerical results are exactly in accord with the analysis in theory.