On the Convergence of Weighted AdaGrad with Momentum for Training Deep Neural Networks

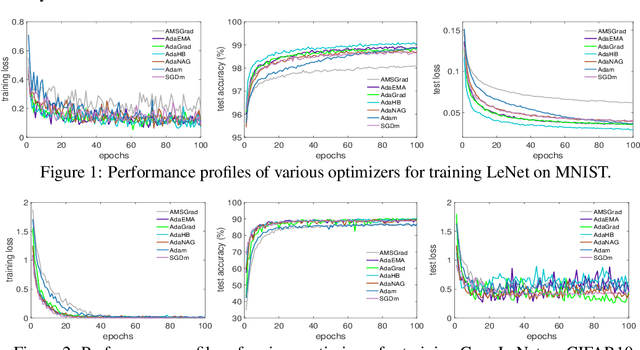
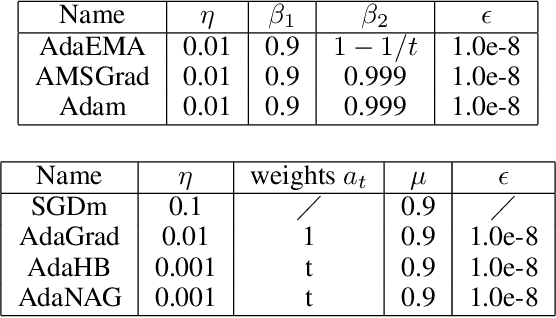
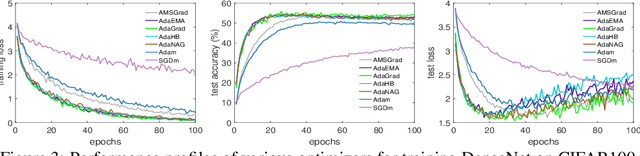
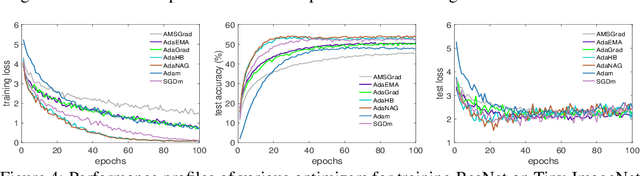
Adaptive stochastic gradient descent methods, such as AdaGrad, RMSProp, Adam, AMSGrad, etc., have been demonstrated efficacious in solving non-convex stochastic optimization, such as training deep neural networks. However, their convergence rates have not been touched under the non-convex stochastic circumstance except recent breakthrough results on AdaGrad, perturbed AdaGrad and AMSGrad. In this paper, we propose two new adaptive stochastic gradient methods called AdaHB and AdaNAG which integrate a novel weighted coordinate-wise AdaGrad with heavy ball momentum and Nesterov accelerated gradient momentum, respectively. The $\mathcal{O}(\frac{\log{T}}{\sqrt{T}})$ non-asymptotic convergence rates of AdaHB and AdaNAG in non-convex stochastic setting are also jointly established by leveraging a newly developed unified formulation of these two momentum mechanisms. Moreover, comparisons have been made between AdaHB, AdaNAG, Adam and RMSProp, which, to a certain extent, explains the reasons why Adam and RMSProp are divergent. In particular, when momentum term vanishes we obtain convergence rate of coordinate-wise AdaGrad in non-convex stochastic setting as a byproduct.