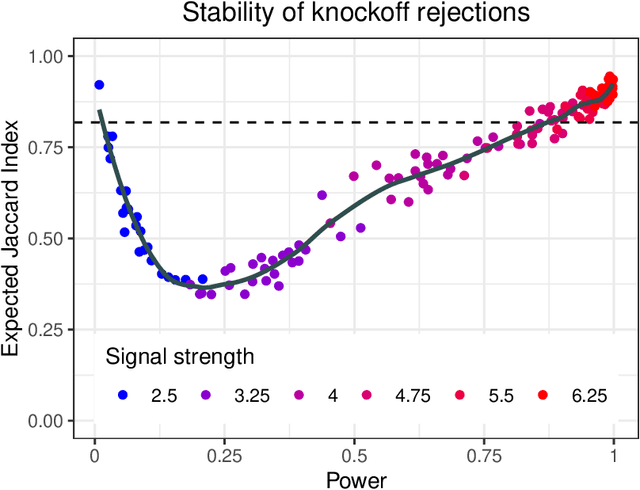
The leave-one-covariate-out conditional randomization test

Conditional independence testing is an important problem, yet provably hard without assumptions. One of the assumptions that has become popular of late is called "model-X", where we assume we know the joint distribution of the covariates, but assume nothing about the conditional distribution of the outcome given the covariates. Knockoffs is a popular methodology associated with this framework, but it suffers from two main drawbacks: only one-bit $p$-values are available for inference on each variable, and the method is randomized with significant variability across runs in practice. The conditional randomization test (CRT) is thought to be the "right" solution under model-X, but usually viewed as computationally inefficient. This paper proposes a computationally efficient leave-one-covariate-out (LOCO) CRT that addresses both drawbacks of knockoffs. LOCO CRT produces valid $p$-values that can be used to control the familywise error rate, and has nearly zero algorithmic variability. For L1 regularized M-estimators, we develop an even faster variant called L1ME CRT, which reuses computation by leveraging a novel observation about the stability of the cross-validated lasso to removing inactive variables. Last, for multivariate Gaussian covariates, we present a closed form expression for the LOCO CRT $p$-value, thus completely eliminating resampling in this important special case.

A theoretical treatment of conditional independence testing under Model-X

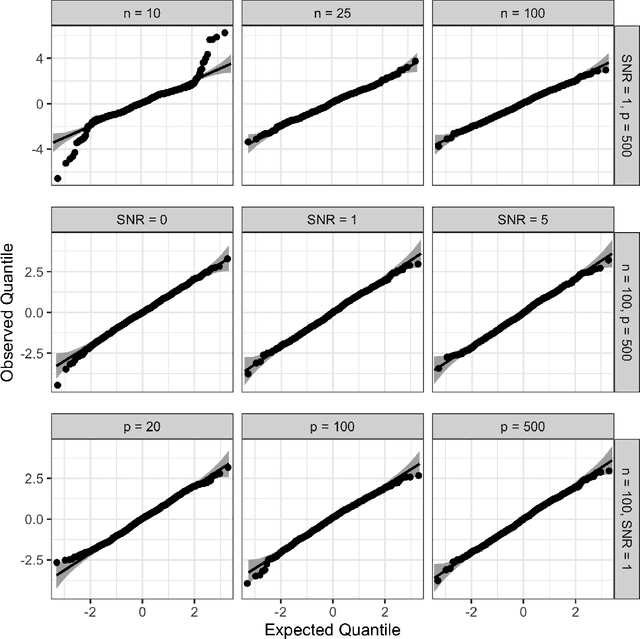
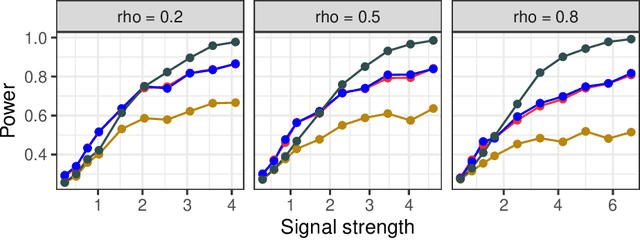
For testing conditional independence (CI) of a response $Y$ and a predictor $X$ given covariates $Z$, the recently introduced model-X (MX) framework has been the subject of active methodological research, especially in the context of MX knockoffs and their successful application to genome-wide association studies. In this paper, we build a theoretical foundation for the MX CI problem, yielding quantitative explanations for empirically observed phenomena and novel insights to guide the design of MX methodology. We focus our analysis on the conditional randomization test (CRT), whose validity conditional on $Y,Z$ allows us to view it as a test of a point null hypothesis involving the conditional distribution of $X$. We use the Neyman-Pearson lemma to derive an intuitive most-powerful CRT statistic against a point alternative as well as an analogous result for MX knockoffs. We define MX analogs of $t$- and $F$- tests and derive their power against local semiparametric alternatives using Le Cam's local asymptotic normality theory, explicitly capturing the prediction error of the underlying machine learning procedure. Importantly, all our results hold conditionally on $Y,Z$, almost surely in $Y,Z$. Finally, we define nonparametric notions of effect size and derive consistent estimators inspired by semiparametric statistics. Thus, this work forms explicit, and underexplored, bridges from MX to both classical statistics (testing) and modern causal inference (estimation).

Covariance estimation using conjugate gradient for 3D classification in Cryo-EM

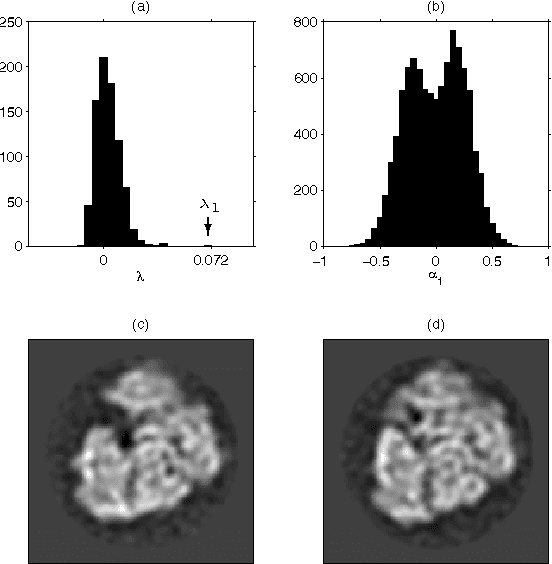
Classifying structural variability in noisy projections of biological macromolecules is a central problem in Cryo-EM. In this work, we build on a previous method for estimating the covariance matrix of the three-dimensional structure present in the molecules being imaged. Our proposed method allows for incorporation of contrast transfer function and non-uniform distribution of viewing angles, making it more suitable for real-world data. We evaluate its performance on a synthetic dataset and an experimental dataset obtained by imaging a 70S ribosome complex.