The leave-one-covariate-out conditional randomization test
Paper and Code
Jul 13, 2020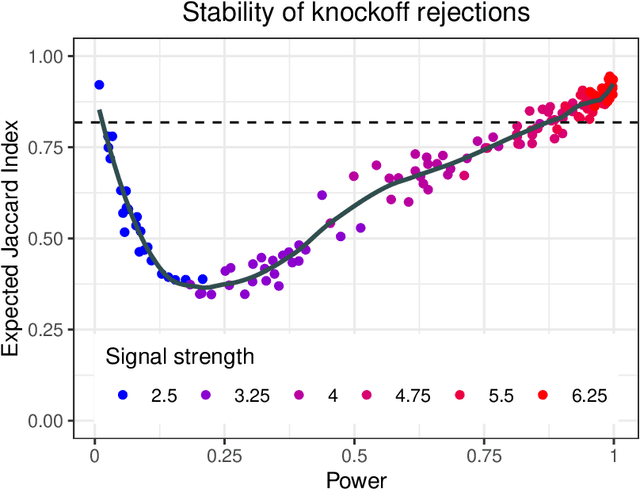

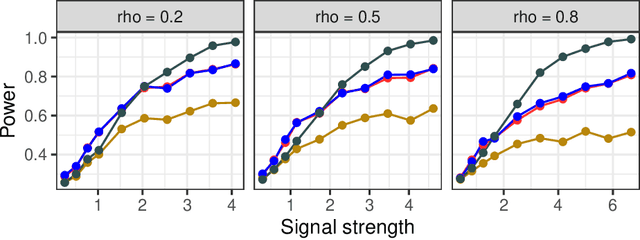

Conditional independence testing is an important problem, yet provably hard without assumptions. One of the assumptions that has become popular of late is called "model-X", where we assume we know the joint distribution of the covariates, but assume nothing about the conditional distribution of the outcome given the covariates. Knockoffs is a popular methodology associated with this framework, but it suffers from two main drawbacks: only one-bit $p$-values are available for inference on each variable, and the method is randomized with significant variability across runs in practice. The conditional randomization test (CRT) is thought to be the "right" solution under model-X, but usually viewed as computationally inefficient. This paper proposes a computationally efficient leave-one-covariate-out (LOCO) CRT that addresses both drawbacks of knockoffs. LOCO CRT produces valid $p$-values that can be used to control the familywise error rate, and has nearly zero algorithmic variability. For L1 regularized M-estimators, we develop an even faster variant called L1ME CRT, which reuses computation by leveraging a novel observation about the stability of the cross-validated lasso to removing inactive variables. Last, for multivariate Gaussian covariates, we present a closed form expression for the LOCO CRT $p$-value, thus completely eliminating resampling in this important special case.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge