Efficient Techniques for Data Reconstruction, with Finite-Width Recovery Guarantees

Data reconstruction attacks on trained neural networks aim to recover the data on which the network has been trained and pose a significant threat to privacy, especially if the training dataset contains sensitive information. Here, we propose a unified optimization formulation of the data reconstruction problem based on initial and trained parameter values, incorporating state-of-the-art proposals. We show that in the random feature model, this formulation provably leads to training data reconstruction with high probability, provided the network width is sufficiently large; this unprecedented finite-width result uses PAC-style bounds. Furthermore, when the data lies in a low-dimensional subspace, we show that the network width requirement for successful reconstruction can be relaxed, with bounds depending on the subspace dimension rather than the ambient dimension. For general neural network models and unknown data orientations, we propose an efficient reconstruction algorithm that approximates the low-dimensional data subspace through the change in the first-layer weights during training and uses only the last-layer weights for reconstruction, thus reducing the search space dimension and the required network width for high-quality reconstructions. Our numerical experiments on synthetic datasets and CIFAR-10 confirm that our subspace-aware reconstruction approach outperforms standard full-space techniques.

Coordinate descent on the orthogonal group for recurrent neural network training

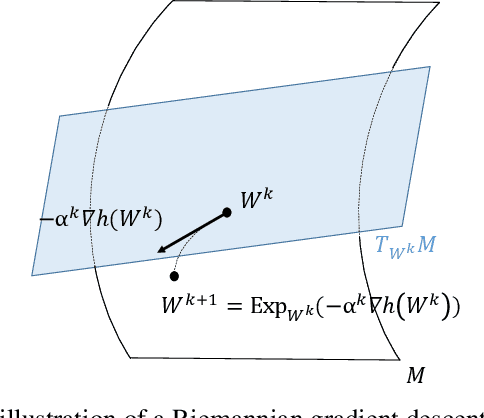
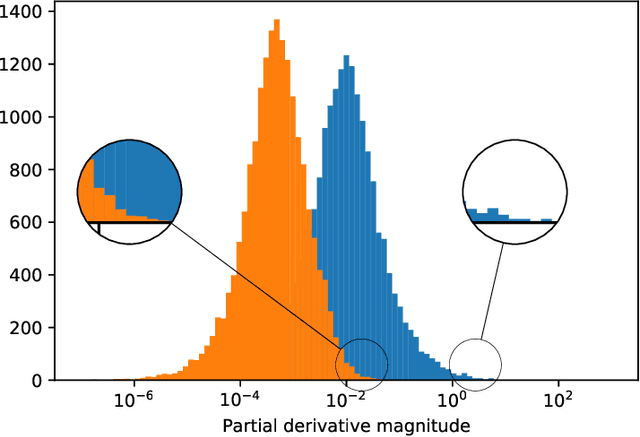
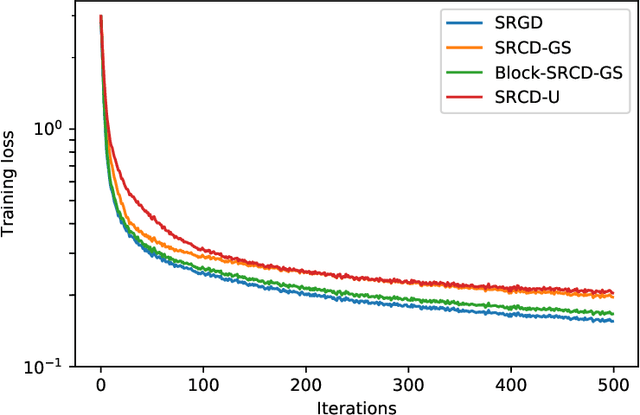
We propose to use stochastic Riemannian coordinate descent on the orthogonal group for recurrent neural network training. The algorithm rotates successively two columns of the recurrent matrix, an operation that can be efficiently implemented as a multiplication by a Givens matrix. In the case when the coordinate is selected uniformly at random at each iteration, we prove the convergence of the proposed algorithm under standard assumptions on the loss function, stepsize and minibatch noise. In addition, we numerically demonstrate that the Riemannian gradient in recurrent neural network training has an approximately sparse structure. Leveraging this observation, we propose a faster variant of the proposed algorithm that relies on the Gauss-Southwell rule. Experiments on a benchmark recurrent neural network training problem are presented to demonstrate the effectiveness of the proposed algorithm.

Global optimization using random embeddings

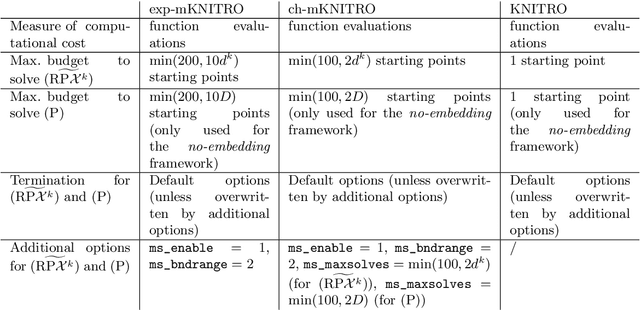
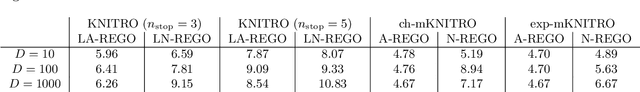
We propose a random-subspace algorithmic framework for global optimization of Lipschitz-continuous objectives, and analyse its convergence using novel tools from conic integral geometry. X-REGO randomly projects, in a sequential or simultaneous manner, the high-dimensional original problem into low-dimensional subproblems that can then be solved with any global, or even local, optimization solver. We estimate the probability that the randomly-embedded subproblem shares (approximately) the same global optimum as the original problem. This success probability is then used to show convergence of X-REGO to an approximate global solution of the original problem, under weak assumptions on the problem (having a strictly feasible global solution) and on the solver (guaranteed to find an approximate global solution of the reduced problem with sufficiently high probability). In the particular case of unconstrained objectives with low effective dimension, that only vary over a low-dimensional subspace, we propose an X-REGO variant that explores random subspaces of increasing dimension until finding the effective dimension of the problem, leading to X-REGO globally converging after a finite number of embeddings, proportional to the effective dimension. We show numerically that this variant efficiently finds both the effective dimension and an approximate global minimizer of the original problem.

Fitting, Comparison, and Alignment of Trajectories on Positive Semi-Definite Matrices with Application to Action Recognition

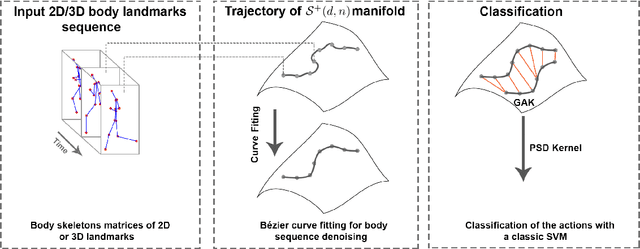
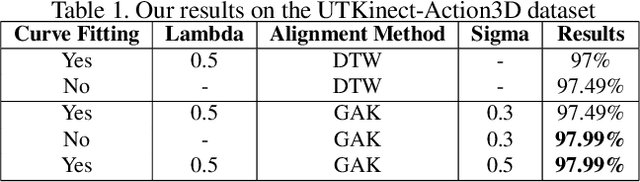
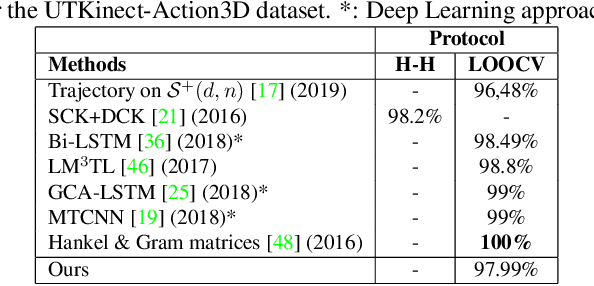
In this paper, we tackle the problem of action recognition using body skeletons extracted from video sequences. Our approach lies in the continuity of recent works representing video frames by Gramian matrices that describe a trajectory on the Riemannian manifold of positive-semidefinite matrices of fixed rank. In comparison with previous works, the manifold of fixed-rank positive-semidefinite matrices is here endowed with a different metric, and we resort to different algorithms for the curve fitting and temporal alignment steps. We evaluated our approach on three publicly available datasets (UTKinect-Action3D, KTH-Action and UAV-Gesture). The results of the proposed approach are competitive with respect to state-of-the-art methods, while only involving body skeletons.